基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法
1.本發明涉及無邊輪運動技術領域,更具體地,給出了一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法。
背景技術:
2.無邊輪是用于模擬足式行走的經典運動機構,將無邊輪機構作為基礎模型來探索足式仿生步態高能效節律運動背后的機構內在特征及先天因素,并在穩定運動的基礎上進一步研究運動的發力機制,可為足式機器人未來實現對人體神經-肌肉-骨骼系統的全面仿生提供依據。
3.發明專利zl202110139486.7和發明專利zl202110138734.6,分別以平面單輪無邊輪模型和非對稱雙輪無邊輪模型為對象,給出了各自在空間斜面的運動行為分析方法;申請號為cn202010890342.0的發明專利,提供了一種針對對稱無邊輪模型斜面地形下的運動行為調節方法;申請號為cn202010890340.1的發明專利,提供了一種非對稱無邊輪模型被動節律行走的穩定性調節方法及系統。在這些方案中,均為在不采用動力源和主動控制的條件下,僅利用無邊輪自身所受重力作用產生沿斜面向下的自發穩定運動行為步態,屬于“被動動態行走”技術,且均為通過調節無邊輪模型自身結構參數或初始運動狀態參數來實現對無邊輪運動行為的調節。
4.綜上,如何在現有技術方案基礎上進一步實現無邊輪的主動發力控制,令無邊輪能夠在平地等非斜坡地形中模擬足式奔跑、跳躍等“主動動態運動”行為,是本領域的重要基礎問題與技術發展方向。
技術實現要素:
5.本發明面向無邊輪的主動發力控制需求,提出基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,該方案通過在無邊輪運動過程中主動調節其支撐腿的剛度實現腿部主動發力,并有效彌補因周期式的足端碰撞而不斷損失的系統能量,為無邊輪持續保持在用戶期望的系統能量狀態提供了一種切實可行的技術方案。
6.為實現上述目的,本發明采用的技術方案為:
7.一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其中無邊輪包括內部輪輻以及輪軸,輪輻繞輪軸旋轉;內部輪輻包括一組腿;無邊輪的總質量為m。
8.腿具有沿其自身軸向發力的能力,發力所采用的具體形式包括沿其自身軸向運動、沿其自身軸向伸縮、依靠沿其自身軸向附加的彈性裝置。
9.采用彈簧負載倒立擺模型來建立單個腿的控制模型,即在控制中將所有的腿均用等效彈簧表示,所有的等效彈簧在自由狀態的長度均為r0,且其初始的剛度均為k。
10.無邊輪在地面的轉動運動過程包含單腿支撐轉動階段和雙腿支撐轉動階段;若任一腿處于支撐狀態,且該腿平行于冠狀面時,則將這一時刻記錄為新的運動步的開始。
11.當無邊輪的運動處于第n步時,將該運動步開始時處于支撐狀態的腿對應的等效
彈簧稱為等效彈簧c,隨著無邊輪轉動運動的持續,當與該腿相鄰的另一腿處于支撐狀態且該另一腿平行于冠狀面時,則記錄為第n步的結束與第n+1步的開始,將該另一腿對應的等效彈簧稱為等效彈簧f;即若無邊輪已經行進至第n步,則代表所有的腿已經共計有n次處于支撐狀態且平行于冠狀面;等效彈簧c、等效彈簧f和無邊輪的集中質量,共同構成雙彈簧負載倒立擺模型。
12.當無邊輪的運動處于第n步時,將該步起始時無邊輪的能量標記為無邊輪的當前步起始能量ecn,將該步結束時無邊輪的能量標記為無邊輪的當前步終止能量efn,將該步運動過程中損失的能量標記為無邊輪的當前步能量損失值δenn,將該步運動過程中主動補償的能量標記為無邊輪的當前步能量補償值δepn,將該步運動過程中為獲得當前步能量補償值δepn而持續施加的補償力標記為無邊輪的當前步補償力fn。
13.在重力加速度為g的重力場中,當無邊輪的運動處于第n步時,無邊輪進行主動發力控制的方法步驟為:
14.步驟1,依據在第n-1步中計算得到的當前步補償力fn,在無邊輪的第n步運動中施加補償力作用;
15.步驟2,依據無邊輪在第n步起始時的質心實時速度vcn、等效彈簧c在第n步起始時的長度rcn、等效彈簧c在第n步起始時與豎直方向的夾角θcn,計算當前步起始能量ecn;
16.步驟3,依據無邊輪在第n步結束時的質心實時速度vfn、等效彈簧f在第n步結束時的長度rfn、等效彈簧f在第n步結束時與豎直方向的夾角θfn,計算當前步終止能量efn;
17.步驟4,依據當前步起始能量ecn、當前步終止能量efn、當前步能量補償值δepn,計算當前步能量損失值δenn;
18.步驟5,依據當前步能量損失值δenn、當前步終止能量efn、期望的下一步終止能量efdes,估算下一步能量補償值δepn+1;
19.步驟6,依據下一步能量補償值δepn+1,計算腿部剛度調節值δk;
20.步驟7,依據腿部剛度調節值δk、等效彈簧c的實時長度rc、等效彈簧f的實時長度rf,計算下一步補償力fn+1;
21.步驟8,無邊輪的第n步運動結束后,將n+1的值賦給n,即同時將fn+1的值賦給fn、將δepn+1的值賦給δepn,回到步驟1循環運行,直至運動任務結束。
22.其中,等效彈簧f在第n步結束時的長度rfn,與第n+1步開始時等效彈簧c的長度rcn+1相等。
23.步驟2中計算當前步起始能量ecn的具體方法為:
24.ecn=m
×
(vcn)2/2+m
×g×
rcn
×
cos(θcn)+k
×
(r0-rcn)2/2;
25.若夾角θcn的值為0,則當前步起始能量ecn的計算方法簡化為:
26.ecn=m
×
(vcn)2/2+m
×g×
rcn+k
×
(r0-rcn)2/2。
27.若無邊輪為簡化的平面無邊輪,且其在水平地面上行進,則夾角θcn的值為0。
28.步驟3中計算當前步終止能量efn的具體方法為:
29.efn=m
×
(vfn)2/2+m
×g×
rfn
×
cos(θfn)+k
×
(r0-rfn)2/2;
30.若夾角θfn的值為0,則當前步終止能量efn的計算方法簡化為:
31.efn=m
×
(vfn)2/2+m
×g×
rfn+k
×
(r0-rfn)2/2。
32.若無邊輪為簡化的平面無邊輪,且其在水平地面上行進,則夾角θfn的值為0。
33.步驟4中計算當前步能量損失值δenn的具體方法為:
34.δenn=ecn+δepn-efn。
35.步驟5中估算下一步能量補償值δepn+1的具體方法為:
36.δepn+1=efdes+δenn-efn。
37.當無邊輪的運動處于第1步時,即n的值為1時,步驟4中的當前步能量補償值δepn的值為:
38.δepn=0。
39.步驟6中計算腿部剛度調節值δk的具體方法為:
40.δk=2
×
(δepn+1)/(r0-rfn)2。
41.步驟7中計算下一步補償力fn+1的一種具體方法為:
42.若僅有等效彈簧c處于支撐狀態,則有
43.fn+1=δk
×
(r0-rc)=2
×
(δepn+1)
×
(r0-rc)/(r0-rfn)2;
44.若僅有等效彈簧f處于支撐狀態,則有
45.fn+1=δk
×
(r0-rf)=2
×
(δepn+1)
×
(r0-rf)/(r0-rfn)2。
46.步驟7中計算下一步補償力fn+1的另一種具體方法為:
47.若僅有等效彈簧c處于支撐狀態,則有
48.fn+1=δk
×
(rc-rfn)=2
×
(δepn+1)
×
(rc-rfn)/(r0-rfn)2;
49.若僅有等效彈簧f處于支撐狀態,則有
50.fn+1=δk
×
(rf-rfn)=2
×
(δepn+1)
×
(rf-rfn)/(r0-rfn)2。
51.步驟1中在無邊輪的第n步運動中施加補償力作用,其具體的作用時段為從第n步的開始時刻起,即從等效彈簧c對應的腿處于支撐狀態且平行于冠狀面時起,直至該腿不再處于支撐狀態。
52.與現有技術相比,本發明具備以下顯著特點:
53.(1)基于雙彈簧負載倒立擺模型,給出了用于保持系統能量穩定的腿部補償力計算與施加方法,不僅能夠實現無邊輪在水平地面、小臺階、階梯等地形中的連續穩定運動,還賦予無邊輪一定的主動抗擾能力。
54.(2)采用了無邊輪沿其腿部連桿軸向發力的方式,這種軸向發力具體可通過剛性腿部沿軸向的快速運動、可伸縮腿部沿軸向的快速伸縮、依靠附加在剛性腿部軸向的彈性裝置作用等多種方式實現,易于實施。
55.(3)能量補償值、腿部剛度調節值、補償力值均為提前預估,整體計算快速,適用于無邊輪快速運動的應用場景。
附圖說明
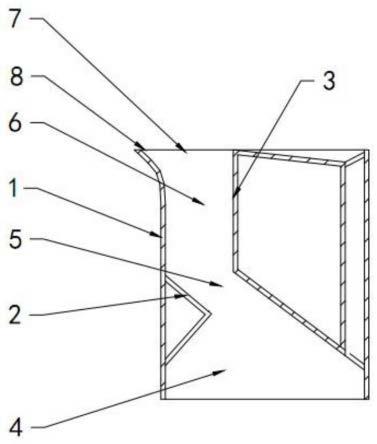
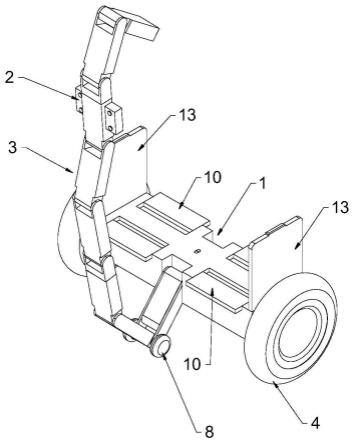
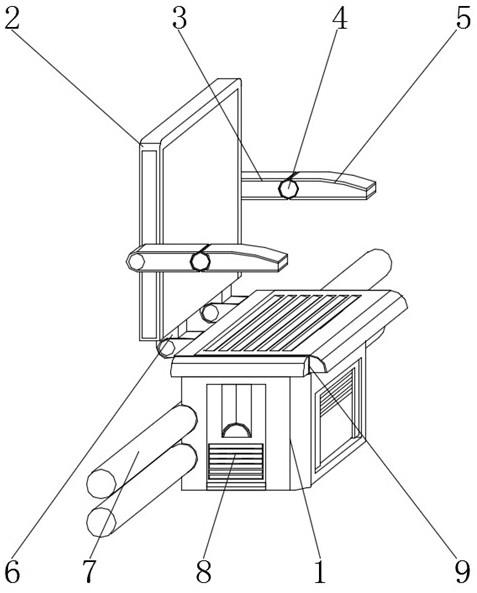
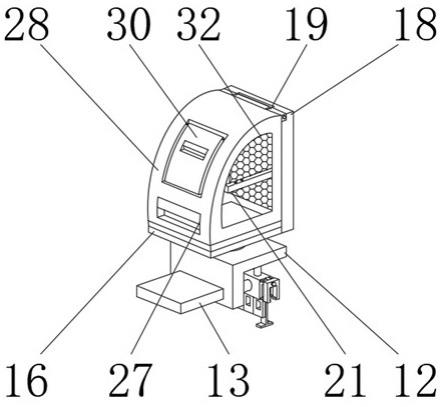
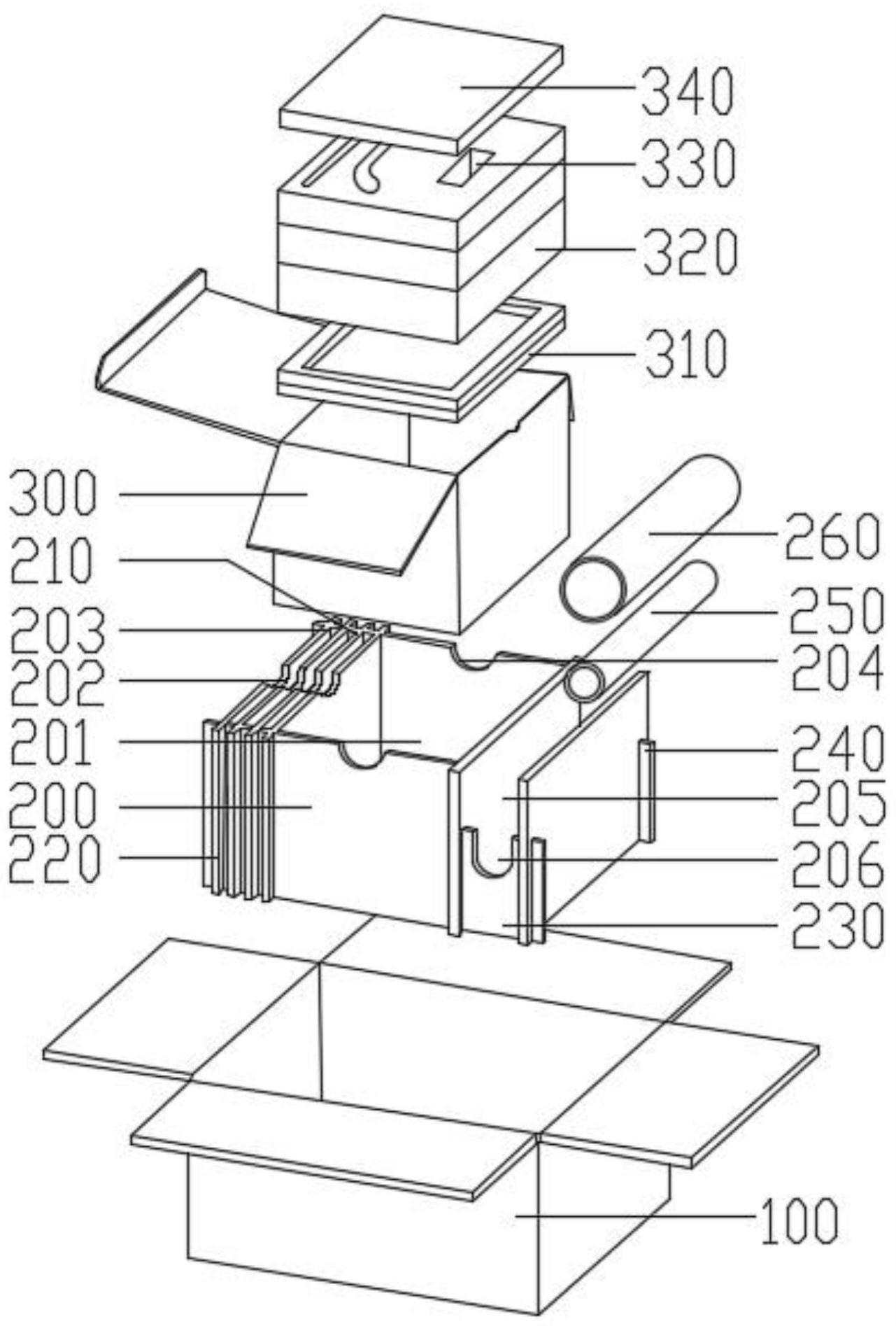
56.圖1為本發明所述無邊輪及其雙彈簧負載倒立擺模型的示意圖。
57.圖2為本發明所述無邊輪主動發力控制方法的流程示意圖。
58.圖3為帶有彈簧的平面無邊輪發力控制實例;其中圖3(a)所示為無邊輪在臺階地形運動過程中系統補償力fn的連續變化示意圖,圖3(b)所示為運動過程中無邊輪沿矢狀面水平方向的速度變化示意圖;圖3(c)所示為平面無邊輪在該臺階地形中的運動情況示意圖;
59.圖3(d)所示為該臺階地形的詳細示意圖。
具體實施方式
60.以下結合實施例和附圖對本發明提出的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法作進一步詳細的說明,但以下實施例僅是說明性的,本發明的保護范圍并不受這些實施例的限制。
61.圖1所示為本發明所述無邊輪及其雙彈簧負載倒立擺模型的示意圖。如圖1所示,本發明中的無邊輪包括內部輪輻以及輪軸,輪輻繞輪軸旋轉;內部輪輻包括一組腿;無邊輪的總質量為m。
62.無邊輪的腿具有沿其自身軸向發力的能力,發力所采用的具體形式包括沿其自身軸向運動、沿其自身軸向伸縮、依靠沿其自身軸向附加的彈性裝置。采用上述任一方式,均可實現沿腿部軸向的發力,即無邊輪的腿部可以為高剛性結構,但具有沿腿連桿方向快速移動的能力,從而依靠足端與地面的快速蹬踏實現發力;無邊輪的腿部自身還可以為彈性結構,可以如同彈簧般沿腿連桿方向伸長或縮短,并從而調節腿部主動發力;無邊輪的腿部還可以為高剛性結構,但沿其腿連桿方向串聯另一彈性裝置,并依靠該彈性裝置的主動伸長或縮短為腿部提供沿腿連桿方向的驅動力。
63.采用彈簧負載倒立擺模型來建立單個腿的控制模型,即在控制中將所有的腿均用等效彈簧表示,所有的等效彈簧在自由狀態的長度均為r0,且其初始的剛度均為k。
64.將無邊輪的前進方向和其與地面垂線方向所構成的平面定義為無邊輪的矢狀面,將與矢狀面垂直且包含其與地面垂線的平面定義為無邊輪的冠狀面。無邊輪在地面的轉動運動過程包含單腿支撐轉動階段和雙腿支撐轉動階段;若任一腿處于支撐狀態,且該腿平行于冠狀面或者該腿連桿位于預先定義的冠狀面內時,則將這一時刻記錄為新的運動步的開始。這里的冠狀面是相對于無邊輪滾動前進方向
65.當無邊輪的運動處于第n步時,將該運動步開始時處于支撐狀態的腿對應的等效彈簧稱為等效彈簧c,隨著無邊輪轉動運動的持續,當與該腿相鄰的另一腿處于支撐狀態且該另一腿平行于冠狀面或位于冠狀面內時,則記錄為第n步的結束與第n+1步的開始,將該另一腿對應的等效彈簧稱為等效彈簧f;即若無邊輪已經行進至第n步,則代表所有的腿已經共計有n次處于支撐狀態且平行于冠狀面;等效彈簧c、等效彈簧f和無邊輪的集中質量,共同構成雙彈簧負載倒立擺模型。
66.當無邊輪的運動處于第n步時,將該步起始時無邊輪的能量標記為無邊輪的當前步起始能量ecn,將該步結束時無邊輪的能量標記為無邊輪的當前步終止能量efn,將該步運動過程中損失的能量標記為無邊輪的當前步能量損失值δenn,將該步運動過程中主動補償的能量標記為無邊輪的當前步能量補償值δepn,將該步運動過程中為獲得當前步能量補償值δepn而持續施加的補償力標記為無邊輪的當前步補償力fn。
67.圖2所示為本發明中無邊輪主動發力控制方法的流程示意圖。如圖2所示,在重力加速度為g的重力場中,當無邊輪在水平地面上的運動處于第n步時,無邊輪進行主動發力控制的方法步驟為:
68.步驟1,依據在第n-1步中計算得到的當前步補償力fn,在無邊輪的第n步運動中施加補償力作用。
69.步驟2,依據無邊輪在第n步起始時的質心實時速度vcn、等效彈簧c在第n步起始時的長度rcn、等效彈簧c在第n步起始時與豎直方向的夾角θcn,計算當前步起始能量ecn。這里的質心實時速度vcn為空間中的速度矢量,即可將其分解為多個分速度。
70.步驟3,依據無邊輪在第n步結束時的質心實時速度vfn、等效彈簧f在第n步結束時的長度rfn、等效彈簧f在第n步結束時與豎直方向的夾角θfn,計算當前步終止能量efn。這里的質心實時速度vfn為空間中的速度矢量,即可將其分解為多個分速度。
71.步驟4,依據當前步起始能量ecn、當前步終止能量efn、當前步能量補償值δepn,計算當前步能量損失值δenn。
72.步驟5,依據當前步能量損失值δenn、當前步終止能量efn、期望的下一步終止能量efdes,估算下一步能量補償值δepn+1。該期望的下一步終止能量efdes,既可以由用戶實時給出,也可以根據預先設定的規則實時計算得到;例如可將當前步終止能量efn的值賦給efdes,以令系統在下一步的能量與當前步能量相對保持恒定。
73.步驟6,依據下一步能量補償值δepn+1,計算腿部剛度調節值δk。
74.步驟7,依據腿部剛度調節值δk、等效彈簧c的實時長度rc、等效彈簧f的實時長度rf,計算下一步補償力fn+1。
75.步驟8,無邊輪的第n步運動結束后,將n+1的值賦給n,即同時將fn+1的值賦給fn、將δepn+1的值賦給δepn,回到步驟1循環運行,直至運動任務結束。
76.其中,等效彈簧f在第n步結束時的長度rfn,與第n+1步開始時等效彈簧c的長度rcn+1相等。
77.步驟2中計算當前步起始能量ecn的具體方法為:
78.ecn=m
×
(vcn)2/2+m
×g×
rcn
×
cos(θcn)+k
×
(r0-rcn)2/2;
79.若夾角θcn的值為0,則當前步起始能量ecn的計算方法簡化為:
80.ecn=m
×
(vcn)2/2+m
×g×
rcn+k
×
(r0-rcn)2/2。
81.對當前步起始能量ecn的計算分為三個部分,分別是系統的動能、重力勢能和彈性勢能,其中默認水平面高度處的重力勢能為零。
82.考慮到質心實時速度vcn可由傳感器檢測獲得,而傳感器通常為具體檢測沿傳感器自身坐標系各方向的分量,因此這里(vcn)2可由各速度分量的平方和計算得到。
83.步驟3中計算當前步終止能量efn的具體方法為:
84.efn=m
×
(vfn)2/2+m
×g×
rfn
×
cos(θfn)+k
×
(r0-rfn)2/2;
85.若夾角θfn的值為0,則當前步終止能量efn的計算方法簡化為:
86.efn=m
×
(vfn)2/2+m
×g×
rfn+k
×
(r0-rfn)2/2。
87.對當前步終止能量efn的計算與對當前步起始能量ecn的計算相似,其也分為三個部分,分別是系統的動能、重力勢能和彈性勢能,其中默認水平面高度處的重力勢能為零。
88.這里(vfn)2的計算與上述(vcn)2的計算相似,在實際中可按傳感器所測得的各速度分量的平方和進行計算。
89.步驟4中計算當前步能量損失值δenn的具體方法為:
90.δenn=ecn+δepn-efn。
91.步驟5中估算下一步能量補償值δepn+1的具體方法為:
92.δepn+1=efdes+δenn-efn。
93.當無邊輪的運動處于第1步時,即n的值為1時,步驟4中的當前步能量補償值δepn的值為:δepn=0。即在按本方法設計程序時,可在程序運行初始階段預先對δep1賦0值。
94.步驟6中計算腿部剛度調節值δk的具體方法為:
95.δk=2
×
(δepn+1)/(r0-rfn)2。
96.步驟7中計算下一步補償力fn+1的一種具體方法為:
97.若僅有等效彈簧c處于支撐狀態,則有
98.fn+1=δk
×
(r0-rc)=2
×
(δepn+1)
×
(r0-rc)/(r0-rfn)2;
99.若僅有等效彈簧f處于支撐狀態,則有
100.fn+1=δk
×
(r0-rf)=2
×
(δepn+1)
×
(r0-rf)/(r0-rfn)2。
101.步驟7中計算下一步補償力fn+1的另一種具體方法為:
102.若僅有等效彈簧c處于支撐狀態,則有
103.fn+1=δk
×
(rc-rfn)=2
×
(δepn+1)
×
(rc-rfn)/(r0-rfn)2;
104.若僅有等效彈簧f處于支撐狀態,則有
105.fn+1=δk
×
(rf-rfn)=2
×
(δepn+1)
×
(rf-rfn)/(r0-rfn)2。
106.上述給出了步驟7中計算下一步補償力fn+1的兩種具體方法,其中后一種方法使得補償力在每一步初始時的值接近于0,隨著無邊輪的繼續滾動,補償力值也隨著等效彈簧c的壓縮被不斷被釋放而逐漸增加,即在每一步中補償力值由小到大逐漸施加;與之相對,若使用前一種方法,在每一步中補償力值由大到小逐漸施加。
107.步驟1中在無邊輪的第n步運動中施加補償力作用,其具體的作用時段為從第n步的開始時刻起,即從等效彈簧c對應的腿處于支撐狀態且平行于冠狀面時起,直至該腿不再處于支撐狀態,或者直至等效彈簧f對應的腿也處于支撐狀態。采用此種施加補償力的時間段方案后,上述步驟7中計算下一步補償力fn+1的具體方法,僅包含僅有等效彈簧c處于支撐狀態的情形。
108.圖3所示為一種帶有彈簧的平面無邊輪在臺階上運動的實例,其中無邊輪采用本發明所給出的主動發力控制方案。包含臺階的地形示意如圖3(d)所示,其中參數h代表臺階的高度,參數x代表臺階的長度,臺階長度均為5m,以下仿真過程跨越的臺階數都均為3;圖3(a)所示為系統補償力fn在運動過程中的連續變化;圖3(b)所示為運動過程中無邊輪沿矢狀面方向的速度變化;圖3(c)所示為平面無邊輪在該臺階地形中的運動情況。平面無邊輪模型由8條伸縮腿以及中心質點組成,每條伸縮腿上都加有彈簧以實現發力控制并模擬人行走時腿蹬踏地面的作用。其中該平面無邊輪的腿長為0.6m,腿部等效彈簧的自由長度r0值為0.15m,等效彈簧的剛度值k為400n/m,無邊輪的總質量m為5kg;該平面無邊輪的初始旋轉角度為0rad,初始旋轉角速度為4.36rad/s,初始的水平速度和豎直速度分別為0.7m/s和0m/s,期望的水平速度和豎直速度分別為1.2m/s和0m/s。在該實例中,當無邊輪剛跨上臺階時,由于重力勢能增加,動能相對減小,因此水平速度減小,下一步態周期所需補償的能量δepn+1增大,施加在支撐腿上的補償力fn+1增大;經過5個步態周期后運動趨于穩定,且水平運動速度又回到1.2m/s左右。運動過程中分別在7.5s,12s,16.5s左右跨越三個臺階,平均跨越一個臺階的時間為4.5s,在一個臺階上運動的平均速度約為1.1m/s,運動的距離與臺階長度相等。若將該地形場景中的臺階看作平地地形中存在的擾動,則此實例還展示出本發明所給出的主動發力控制方案不僅能夠實現無邊輪在水平地面、階梯等地形中的連續
穩定運動,還賦予無邊輪一定的主動抗擾能力。
技術特征:
1.一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述無邊輪,包括內部輪輻以及輪軸,輪輻繞輪軸旋轉;所述內部輪輻包括一組腿;所述無邊輪的總質量為m;所述腿具有沿其自身軸向發力的能力,所述發力所采用的具體形式包括沿其自身軸向運動、沿其自身軸向伸縮、依靠沿其自身軸向附加的彈性裝置;采用彈簧負載倒立擺模型來建立單個所述腿的控制模型,即在控制中將所有的所述腿均用等效彈簧表示,所有的所述等效彈簧在自由狀態的長度均為r0,且其初始的剛度均為k;所述無邊輪在地面的轉動運動過程包含單腿支撐轉動階段和雙腿支撐轉動階段;若任一所述腿處于支撐狀態,且該所述腿平行于冠狀面時,則將這一時刻記錄為新的運動步的開始;當所述無邊輪的運動處于第n步時,將該運動步開始時處于支撐狀態的所述腿對應的等效彈簧稱為等效彈簧c,隨著所述無邊輪轉動運動的持續,當與該所述腿相鄰的另一所述腿處于支撐狀態且該另一所述腿平行于冠狀面時,則記錄為第n步的結束與第n+1步的開始,將該另一所述腿對應的等效彈簧稱為等效彈簧f;即若所述無邊輪已經行進至第n步,則代表所有的所述腿已經共計有n次處于支撐狀態且平行于冠狀面;所述等效彈簧c、等效彈簧f和所述無邊輪的集中質量,共同構成所述雙彈簧負載倒立擺模型;當所述無邊輪的運動處于第n步時,將該步起始時所述無邊輪的能量標記為所述無邊輪的當前步起始能量ecn,將該步結束時所述無邊輪的能量標記為所述無邊輪的當前步終止能量efn,將該步運動過程中損失的能量標記為所述無邊輪的當前步能量損失值δenn,將該步運動過程中主動補償的能量標記為所述無邊輪的當前步能量補償值δepn,將該步運動過程中為獲得所述當前步能量補償值δepn而持續施加的補償力標記為所述無邊輪的當前步補償力fn;在重力加速度為g的重力場中,當所述無邊輪的運動處于第n步時,所述無邊輪進行主動發力控制的方法步驟為:步驟1,依據在第n-1步中計算得到的所述當前步補償力fn,在所述無邊輪的第n步運動中施加補償力作用;步驟2,依據所述無邊輪在第n步起始時的質心實時速度vcn、等效彈簧c在第n步起始時的長度rcn、等效彈簧c在第n步起始時與豎直方向的夾角θcn,計算所述當前步起始能量ecn;步驟3,依據所述無邊輪在第n步結束時的質心實時速度vfn、等效彈簧f在第n步結束時的長度rfn、等效彈簧f在第n步結束時與豎直方向的夾角θfn,計算所述當前步終止能量efn;步驟4,依據所述當前步起始能量ecn、當前步終止能量efn、當前步能量補償值δepn,計算所述當前步能量損失值δenn;步驟5,依據所述當前步能量損失值δenn、所述當前步終止能量efn、期望的下一步終止能量efdes,估算下一步能量補償值δepn+1;步驟6,依據所述下一步能量補償值δepn+1,計算腿部剛度調節值δk;步驟7,依據所述腿部剛度調節值δk、等效彈簧c的實時長度rc、等效彈簧f的實時長度
rf,計算下一步補償力fn+1;步驟8,所述無邊輪的第n步運動結束后,將n+1的值賦給n,即同時將fn+1的值賦給fn、將δepn+1的值賦給δepn,回到步驟1循環運行,直至運動任務結束;其中,所述等效彈簧f在第n步結束時的長度rfn,與第n+1步開始時等效彈簧c的長度rcn+1相等。2.根據權利要求1所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟2中計算所述當前步起始能量ecn的具體方法為:ecn=m
×
(vcn)2/2+m
×
g
×
rcn
×
cos(θcn)+k
×
(r0-rcn)2/2;若所述夾角θcn的值為0,則所述當前步起始能量ecn的計算方法簡化為:ecn=m
×
(vcn)2/2+m
×
g
×
rcn+k
×
(r0-rcn)2/2。3.根據權利要求1所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟3中計算所述當前步終止能量efn的具體方法為:efn=m
×
(vfn)2/2+m
×
g
×
rfn
×
cos(θfn)+k
×
(r0-rfn)2/2;若所述夾角θfn的值為0,則所述當前步終止能量efn的計算方法簡化為:efn=m
×
(vfn)2/2+m
×
g
×
rfn+k
×
(r0-rfn)2/2。4.根據權利要求1所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟4中計算所述當前步能量損失值δenn的具體方法為:δenn=ecn+δepn-efn。5.根據權利要求1所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟5中估算所述下一步能量補償值δepn+1的具體方法為:δepn+1=efdes+δenn-efn。6.根據權利要求5所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:當所述無邊輪的運動處于第1步時,即n的值為1時,所述步驟4中的所述當前步能量補償值δepn的值為:δepn=0。7.根據權利要求1所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟6中計算所述腿部剛度調節值δk的具體方法為:δk=2
×
(δepn+1)/(r0-rfn)2。8.根據權利要求7所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟7中計算所述下一步補償力fn+1的一種具體方法為:若僅有所述等效彈簧c處于支撐狀態,則有fn+1=δk
×
(r0-rc)=2
×
(δepn+1)
×
(r0-rc)/(r0-rfn)2;
若僅有所述等效彈簧f處于支撐狀態,則有fn+1=δk
×
(r0-rf)=2
×
(δepn+1)
×
(r0-rf)/(r0-rfn)2。9.根據權利要求7所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟7中計算所述下一步補償力fn+1的一種具體方法為:若僅有所述等效彈簧c處于支撐狀態,則有fn+1=δk
×
(rc-rfn)=2
×
(δepn+1)
×
(rc-rfn)/(r0-rfn)2;若僅有所述等效彈簧f處于支撐狀態,則有fn+1=δk
×
(rf-rfn)=2
×
(δepn+1)
×
(rf-rfn)/(r0-rfn)2。10.根據權利要求1所述的一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法,其特征在于:所述步驟1中在所述無邊輪的第n步運動中施加補償力作用,其具體的作用時段為從第n步的開始時刻起,即從所述等效彈簧c對應的所述腿處于支撐狀態且平行于冠狀面時起,直至該所述腿不再處于支撐狀態。
技術總結
本發明涉及一種基于雙彈簧負載倒立擺模型的無邊輪主動發力控制方法。該方法以無邊輪的每一個運動步為周期,循環運行;并將每一個運動步起始時的支撐腿和該運動步結束時的支撐腿各自等效為一個彈簧,從而將這兩個等效彈簧和無邊輪的集中質量共同構成雙彈簧負載倒立擺模型。基于該雙彈簧負載倒立擺模型的主動發力控制方法包含八個主要步驟,分別為施加補償力、計算當前步起始能量、計算當前步終止能量、計算當前步能量損失值、估算下一步能量補償值、計算腿部剛度調節值、計算下一步補償力、循環內賦值。本發明給出了用于保持無邊輪系統能量穩定的腿部補償力計算及施加方法,整體計算快速,能夠實現無邊輪在水平地面、階梯等地形中的連續穩定運動。形中的連續穩定運動。形中的連續穩定運動。