一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法與流程
1.本發(fā)明涉及結(jié)構(gòu)動(dòng)力學(xué)分析技術(shù)領(lǐng)域,具體涉及一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法。
背景技術(shù):
2.提升機(jī)主軸是礦井提升機(jī)的核心組件,不僅承擔(dān)在提升中產(chǎn)生的扭矩,還要承受鋼絲繩的張力,在長(zhǎng)時(shí)間高負(fù)荷工作后,主軸關(guān)鍵位置出現(xiàn)疲勞損壞的概率會(huì)大大增加,直接影響提升機(jī)的工作性能,嚴(yán)重可能危及工作人員的生命安全。此外,提升機(jī)主軸具有階梯式結(jié)構(gòu),采用現(xiàn)有方法建模會(huì)產(chǎn)生較大誤差。因此,研究基于提升機(jī)主軸結(jié)構(gòu)特點(diǎn)的先進(jìn)建模方法,同時(shí)掌握其力學(xué)性能具有重要的現(xiàn)實(shí)意義。
3.傳統(tǒng)的梁理論和實(shí)體單元建模方法計(jì)算量呈量級(jí)增長(zhǎng),求解過程復(fù)雜,在計(jì)算短軸時(shí)會(huì)產(chǎn)生較大的誤差,并且無法采用現(xiàn)有的一維優(yōu)化設(shè)計(jì)算法,所以不適合工程應(yīng)用。
技術(shù)實(shí)現(xiàn)要素:
4.針對(duì)上述存在的技術(shù)不足,本發(fā)明的目的是提供一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法。
5.為解決上述技術(shù)問題,本發(fā)明采用如下技術(shù)方案:
6.本發(fā)明提供一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,包括以下步驟:
7.(1)求解提升機(jī)主軸變形的徑向位移u
ρ
(x,y,z;t)、切向位移和軸向翹曲uz(x,y,z;t);
8.(2)建立主軸段的三維cartesian坐標(biāo)系,根據(jù)建立的坐標(biāo)系,用步驟(1) 求解的三個(gè)位移分量表示主軸段的位移場(chǎng);
9.(3)引入carrera通用格式,根據(jù)一維梁理論,將步驟(2)的主軸位移場(chǎng)采用張量表示,然后基于二元級(jí)數(shù)展開,主軸上一點(diǎn)與z軸的垂直距離ρ在柱坐標(biāo)系下用矩陣形式表示廣義坐標(biāo)向量ψ;
10.(4)根據(jù)經(jīng)典彈性力學(xué)理論,小位移變形情況下,由步驟3求出的主軸位移場(chǎng),在柱坐標(biāo)系下表示出線性微分算子c,由hooke定律求出應(yīng)力向量σ,計(jì)算本構(gòu)矩陣e;
11.(5)根據(jù)虛位移原理,由應(yīng)變能公式、勢(shì)能公式和動(dòng)能公式分別計(jì)算出主軸的應(yīng)變能、勢(shì)能和動(dòng)能,采用hamilton原理,得到相應(yīng)的控制微分方程;
12.(6)運(yùn)用插值函數(shù),表示出節(jié)點(diǎn)的廣義位移d,帶入步驟(5)中的微分控制方程,化簡(jiǎn)得到最終結(jié)果;
13.(7)根據(jù)步驟(1)-步驟(6),利用matlab求出提升機(jī)主軸的總體質(zhì)量矩陣和總體剛度矩陣,進(jìn)一步求解可得到主軸的固有頻率,將該計(jì)算結(jié)果與 ansys模擬得到的結(jié)果進(jìn)行對(duì)比,驗(yàn)證提升機(jī)主軸的動(dòng)力學(xué)建模方法的準(zhǔn)確性。
14.優(yōu)選地,所述步驟(2)中位移場(chǎng)為:
15.u(x,y,z;t)=ψi(x,z)ui(y;t)i=1,2,
…
,n;
16.其中ψi是廣義坐標(biāo)向量,是截面上坐標(biāo)x和z的函數(shù),ui是廣義位移向量, n是展開式項(xiàng)數(shù),下標(biāo)i表示張量疊加。
17.優(yōu)選地,所述廣義位移向量ui表示為:
18.u
x
=u1+xu2+yu3+x2u4+xyu5+y2u6;
19.uy=v1+xv2+yv3+x
2v4
+xyv5+y
2v6
;
20.uz=w1+xw2+yw3+x2w4+xyw5+y2w6;
21.根據(jù)極坐標(biāo)與直角坐標(biāo)的轉(zhuǎn)換為:
[0022][0023]
其中x、y表示主軸截面的坐標(biāo),ρ、表示主軸在柱坐標(biāo)系下的坐標(biāo),u
x
、 uy、uz表示主軸任意一點(diǎn)在直角坐標(biāo)系下三個(gè)方向的位移分量,u
ρ
、表示主軸在柱坐標(biāo)下ρ軸和軸的位移分量,u1~u6表示x軸方向的6個(gè)廣義位移, v1~v6表示y軸方向的6個(gè)廣義位移,w1~w6表示z軸方向的6個(gè)廣義位移。
[0024]
主軸廣義坐標(biāo)向量ψi選用的是由n階基函數(shù)xiyj構(gòu)成的二元taylor多項(xiàng)式,當(dāng)下標(biāo)張量i=2時(shí),ψ=ψ2,其中ψ參數(shù)表示為:
[0025][0026]
其中:
[0027][0028][0029][0030][0031]
其中ψ表示下標(biāo)張量為2的廣義坐標(biāo)向量,ρ、表示主軸在柱坐標(biāo)系下的坐標(biāo)。
[0032]
優(yōu)選地,步驟(4)中線性微分算子矩陣c表示為:
[0033][0034]
根據(jù)hooke定律,應(yīng)力向量σ表示為:
[0035]
σ=eε;
[0036]
式中:為應(yīng)變向量;其中ε表示應(yīng)變向量,εr、εz表示主軸在柱坐標(biāo)系下三個(gè)方向的線應(yīng)變,γ
rz
、表示主軸在柱坐標(biāo)系下的三個(gè)角應(yīng)變,c表示線性微分算子矩陣,u表示主軸在柱坐標(biāo)系下的位移場(chǎng);
[0037][0038]
其中σ表示應(yīng)力向量,σr、σz表示主軸在柱坐標(biāo)系下三個(gè)方向的正應(yīng)力,σ
rz
、表示主軸在柱坐標(biāo)系下的三個(gè)切應(yīng)力;
[0039]
利用上述公式得出:
[0040]
本構(gòu)矩陣e為:
[0041][0042]
λ和μ分別記為:
[0043]
其中λ和μ是lame常數(shù),e表示材料的彈性模量,ν表示材料的泊松比。
[0044]
優(yōu)選地,步驟(5)中應(yīng)變能、勢(shì)能和動(dòng)能分別表示為u、u
p
和t,根據(jù)hamiltion原理,采用以下公式推導(dǎo)出相應(yīng)的控制微分方程:
[0045][0046][0047][0048]
其中λ是軸長(zhǎng)區(qū)間,α是截面面域,ω表示軸段截面,u是廣義位移向量, p是體分布力向量,q是表面分布力向量,z1,z2(z1《z2)是軸兩端的軸向坐標(biāo),是端面上應(yīng)力向量,()表示端面上的物理量,表示徑向應(yīng)力分量,表示軸向應(yīng)力分量,η表示材料密度,t表示主軸運(yùn)動(dòng)時(shí)間,r表示軸段半徑;
[0049][0050]
根據(jù)hamiltion原理:
[0051][0052]
其中δ表示變分運(yùn)算,t表示運(yùn)動(dòng)時(shí)間,u表示主軸位移場(chǎng);
[0053]
導(dǎo)出控制微分方程為:
[0054][0055]
優(yōu)選地,步驟(6)中節(jié)點(diǎn)廣義位移和插值函數(shù)分別記為d和n,帶入控制微分方程并化簡(jiǎn)得到最終結(jié)果的過程如下;
[0056]
d是節(jié)點(diǎn)廣義位移;
[0057]
d={d
u1t d
v1t d
w1t d
u2t d
v2t d
w2t
}
t
;
[0058]du(1)
={u
1(1)
…u6(1)
}
t
,d
v(1)
={v
1(1)
…v6(1)
}
t
,d
w(1)
={w
1(1)
…w6(1)
}
t
;
[0059]du(2)
={u
1(2)
…u6(2)
}
t
,d
v(2)
={v
1(2)
…v6(2)
}
t
,d
w(2)
={w
1(2)
…w6(2)
}
t
;
[0060]
采用c0插值函數(shù):
[0061]
u=nd=[n
1 n2]d;
[0062][0063][0064]
其中n是插值函數(shù),d是節(jié)點(diǎn)廣義位移,ξ是單元內(nèi)的自然坐標(biāo),其取值區(qū)間為[-1,1];
[0065]
帶入控制微分方程并化簡(jiǎn)得:
[0066][0067]
其中表示端面上的插值函數(shù),()表示端面上的物理量;
[0068]
整理為:
[0069][0070][0071][0072][0073]
其中jacobian函數(shù)j=l/2,l為軸段軸向長(zhǎng)度積分空間,m為質(zhì)量矩陣,k 為剛度矩陣,f為邊界條件。
[0074]
本發(fā)明的有益效果在于:
[0075]
(1)本發(fā)明提供的提升機(jī)主軸建模方法相比于傳統(tǒng)的梁理論和實(shí)體單元建模方法具有更高的計(jì)算效率,適用范圍廣,為提升機(jī)主軸動(dòng)力學(xué)設(shè)計(jì)提供了一種新的設(shè)計(jì)方法。
[0076]
(2)本發(fā)明對(duì)于提升機(jī)主軸建模立的動(dòng)力學(xué)模型與傳統(tǒng)的梁理論和實(shí)體單元建模相比,精度得到提高,方法可靠。
[0077]
(3)本發(fā)明提供的提升機(jī)主軸建模方法具有一般性,適用于任意截面形狀的軸類結(jié)構(gòu)。
附圖說明
[0078]
為了更清楚地說明本發(fā)明實(shí)施例或現(xiàn)有技術(shù)中的技術(shù)方案,下面將對(duì)實(shí)施例或現(xiàn)有技術(shù)描述中所需要使用的附圖作簡(jiǎn)單地介紹,顯而易見地,下面描述中的附圖僅僅是本發(fā)明的一些實(shí)施例,對(duì)于本領(lǐng)域普通技術(shù)人員來講,在不付出創(chuàng)造性勞動(dòng)的前提下,還可以根據(jù)這些附圖獲得其他的附圖。
[0079]
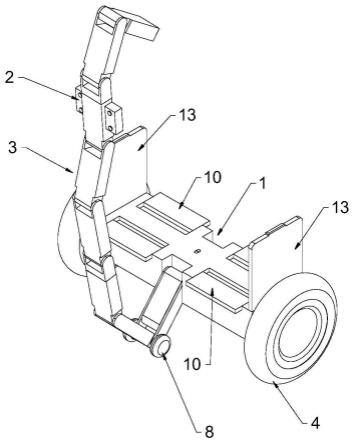
圖1為多繩摩擦式提升機(jī)主軸裝置示意圖;
[0080]
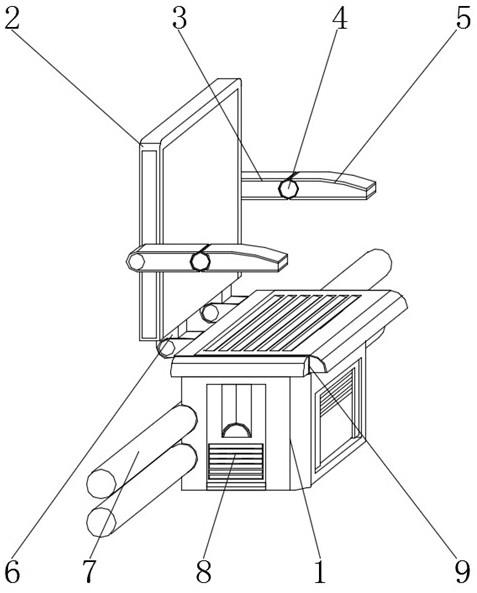
圖2為多繩摩擦式提升機(jī)主軸機(jī)械結(jié)構(gòu)圖;
[0081]
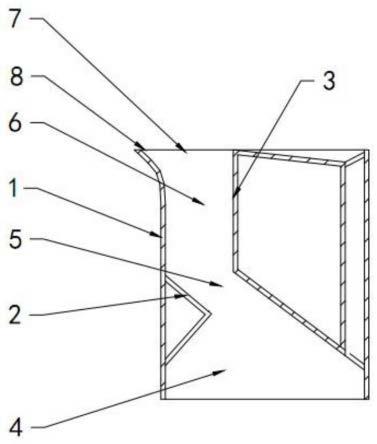
圖3為階梯狀主軸結(jié)構(gòu)及坐標(biāo)系統(tǒng);
[0082]
圖4為梁?jiǎn)卧灰茍?chǎng)的軸向插值與截面擴(kuò)展示意圖;
[0083]
圖5為ansys模型和文本模型計(jì)算結(jié)果對(duì)比圖。
具體實(shí)施方式
[0084]
下面將結(jié)合本發(fā)明實(shí)施例中的附圖,對(duì)本發(fā)明實(shí)施例中的技術(shù)方案進(jìn)行清楚、完整地描述,顯然,所描述的實(shí)施例僅僅是本發(fā)明一部分實(shí)施例,而不是全部的實(shí)施例。基于本發(fā)明中的實(shí)施例,本領(lǐng)域普通技術(shù)人員在沒有做出創(chuàng)造性勞動(dòng)前提下所獲得的所有其他實(shí)施例,都屬于本發(fā)明保護(hù)的范圍。
[0085]
如圖1至圖5所示,本實(shí)施例提供一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,包括如下步驟:
[0086]
(1)在基于有限單元法的基礎(chǔ)上,分別采用徑向位移、切向位移和軸向翹曲來表示提升機(jī)主軸的變形情況,分別求解對(duì)應(yīng)的位移分量;
[0087]
(2)根據(jù)所求解的位移分量建立主軸軸段的三維cartesian坐標(biāo)系,將徑向位移、切向位移和軸向翹曲在該坐標(biāo)系下表示,根據(jù)carrera一元化理論,基于二元級(jí)數(shù)展開,主軸位移場(chǎng)寫成張量形式;
[0088]
(3)建立極坐標(biāo)系,根據(jù)極坐標(biāo)與直角坐標(biāo)的轉(zhuǎn)換關(guān)系,在極坐標(biāo)系下表示主軸軸段位移場(chǎng);
[0089]
(4)根據(jù)經(jīng)典彈性力學(xué)理論,表示出應(yīng)變向量和應(yīng)力向量,由柱坐標(biāo)系下的幾何方程,求解出線性微分算子,由hooke定律,求出本構(gòu)矩陣;
[0090]
(5)由公式計(jì)算應(yīng)變能、勢(shì)能和動(dòng)能,根據(jù)虛位移原理和hamilton原理求解出主軸軸段位移場(chǎng)的控制微分方程;
[0091]
(6)采用插值函數(shù),用節(jié)點(diǎn)廣義位移表示出廣義位移向量,帶入控制微分方程并化簡(jiǎn)得到最終控制方程;
[0092]
(7)利用matlab求出提升機(jī)主軸的總體質(zhì)量矩陣和總體剛度矩陣,進(jìn)一步求解可得到主軸的固有頻率,將該計(jì)算結(jié)果與ansys模擬得到的結(jié)果進(jìn)行對(duì)比,證明提升機(jī)主軸的動(dòng)力學(xué)建模方法的可靠性。
[0093]
以圖1所示的提升機(jī)主軸為對(duì)象進(jìn)行動(dòng)力學(xué)建模,具體實(shí)施步驟如下:
[0094]
步驟1:求解提升機(jī)主軸變形模式分為徑向位移u
ρ
(x,y,z;t)、切向位移和軸向翹曲uz(x,y,z;t)。
[0095]
步驟2:如圖3所示,建立主軸段的三維cartesian坐標(biāo)系,根據(jù)建立的坐標(biāo)系,用三個(gè)位移分量表示主軸段的位移場(chǎng)。
[0096]
步驟3:如圖4所示,引入carrera通用格式,根據(jù)一維梁理論,將主軸位移場(chǎng)采用張量表示,然后基于二元級(jí)數(shù)展開,ρ在柱坐標(biāo)系下用矩陣形式表示廣義坐標(biāo)向量ψ。
[0097]
步驟4:根據(jù)經(jīng)典彈性力學(xué)理論,小位移變形情況下,在柱坐標(biāo)系下表示出線性微分算子c,由hooke定律求出應(yīng)力向量σ,計(jì)算本構(gòu)矩陣e。
[0098]
步驟5:根據(jù)虛位移原理,由公式計(jì)算出應(yīng)變能、勢(shì)能和動(dòng)能,采用hamilton 原理,得到相應(yīng)的控制微分方程。
[0099]
步驟6:運(yùn)用插值函數(shù),表示出節(jié)點(diǎn)的廣義位移d,帶入微分控制方程,化簡(jiǎn)得到最終結(jié)果。
[0100]
步驟7:如圖5所示,利用matlab求解該建模方法提升機(jī)主軸的固有頻率,然后與ansys所求的結(jié)果進(jìn)行對(duì)比分析,驗(yàn)證提升機(jī)主軸動(dòng)力學(xué)建模的準(zhǔn)確性。所述提升機(jī)主軸物理參數(shù)為密度η=7850kg/m3,彈性模量e=2.06
×
10
11
pa,泊松比v=0.3。
[0101]
具體的,所述步驟1中徑向位移u
ρ
(x,y,z;t)、切向位移和軸向翹曲 uz(x,y,z;t)三個(gè)位移向量分別表示為:
[0102][0103]
具體的,所述步驟3位移場(chǎng)u(x,y,z;t)張量表示為:
[0104]
u(x,y,z;t)=ψi(x,z)ui(y;t)i=1,2,
…
,n
[0105]
其中ψi是廣義坐標(biāo)向量,是截面上坐標(biāo)x和z的函數(shù),ui是廣義位移向量,n 是展開式項(xiàng)數(shù),下標(biāo)i表示張量疊加。
[0106]
具體的,所述廣義位移向量ui可表示為:
[0107]ux
=u1+xu2+yu3+x2u4+xyu5+y2u6[0108]
uy=v1+xv2+yv3+x
2v4
+xyv5+y
2v6
[0109]
uz=w1+xw2+yw3+x2w4+xyw5+y2w6[0110]
根據(jù)極坐標(biāo)與直角坐標(biāo)的轉(zhuǎn)換關(guān)系:
[0111][0112]
采用矩陣形式表示ψ:
[0113][0114]
其中ω
11
、ω
12
、ω
21
、ω
22
、ω3分別表示為
[0115][0116][0117][0118][0119][0120]
具體的,所述步驟4中應(yīng)變向量ε和應(yīng)力向量σ分別表示為:
[0121]
[0122][0123]
在小位移變形情況下,柱坐標(biāo)系下的幾何方程為:
[0124]
ε=cu
[0125]
線性微分算子矩陣c表示為:
[0126][0127]
根據(jù)hooke定律,應(yīng)力向量σ表示為:
[0128]
σ=eε
[0129]
本構(gòu)矩陣e記為:
[0130][0131]
其中λ和μ是lame常數(shù),由材料的彈性模量e和泊松比ν決定,分別記為:
[0132][0133]
具體的,應(yīng)變能、勢(shì)能和動(dòng)能分別表示為u、u
p
和t:
[0134][0135][0136][0137]
其中λ是軸長(zhǎng)區(qū)間,α是截面面域,p是體分布力向量,q是表面分布力向量,z1,z2(z1《z2)是軸兩端的軸向坐標(biāo),是端面上應(yīng)力向量,η表示材料密度,() 表示端面上的物理量。
[0138][0139]
hamiltion原理表示為:
[0140][0141]
根據(jù)上述條件,導(dǎo)出微分控制方程
[0142]
[0143]
具體的,所述步驟6中節(jié)點(diǎn)廣義位移和插值函數(shù)分別記為d和n:
[0144]
d={d
u1t d
v1t d
w1t d
u2t d
v2t d
w2t
}
t
[0145]du(1)
={u
1(1)
…u6(1)
}
t
,d
v(1)
={v
1(1)
…v6(1)
}
t
,d
w(1)
={w
1(1)
…w6(1)
}
t
[0146]du(2)
={u
1(2)
…u6(2)
}
t
,d
v(2)
={v
1(2)
…v6(2)
}
t
,d
w(2)
={w
1(2)
…w6(2)
}
t
[0147]
采用c0插值函數(shù)
[0148]
u=nd=[n
1 n2]d
[0149][0150]
式中
[0151]
帶入控制微分方程并化簡(jiǎn)得:
[0152][0153]
運(yùn)動(dòng)微分方程表達(dá)式為:
[0154][0155][0156][0157][0158]
其中jacobian函數(shù)j=l/2,m為質(zhì)量矩陣,k為剛度矩陣,f為邊界條件。所述ansys建立的實(shí)體單元模型采用高階三維20節(jié)點(diǎn)固體結(jié)構(gòu)單元(solid186)進(jìn)行單元?jiǎng)澐郑S向劃分單元數(shù)目為20個(gè),基于級(jí)數(shù)展開的建模方法主軸截面擴(kuò)展函數(shù)ψi選用的是由n階基函數(shù)xiyj構(gòu)成的二元taylor多項(xiàng)式,其中n=2,采用40個(gè)等長(zhǎng)梁?jiǎn)卧M(jìn)行數(shù)值求解。
[0159]
本實(shí)施例運(yùn)用carrera通用表達(dá)格式描述階梯軸軸段位移場(chǎng),采用級(jí)數(shù)展開的方法建立截面位移場(chǎng),然后運(yùn)用hamiltion原理建立主軸軸段運(yùn)動(dòng)微分方程,得到控制微分方程,最后利用線性lagrange插值函數(shù)構(gòu)建一維動(dòng)力學(xué)分析單元,得到有限單元擴(kuò)展的四指標(biāo)基礎(chǔ)矩陣,以hamiltion原理為基礎(chǔ),結(jié)合有限單元法構(gòu)建動(dòng)力學(xué)模型,將模型計(jì)算出的提升機(jī)主軸固有頻率與 ansys計(jì)算結(jié)果進(jìn)行對(duì)比,檢驗(yàn)了該建模方法的可靠性;本實(shí)施例提出的提升機(jī)主軸建模方法在相同精度的條件下有著更高的計(jì)算經(jīng)濟(jì)性,對(duì)于不同結(jié)構(gòu)的提升機(jī)主軸,只需修改相應(yīng)的模型參數(shù),無需重新建模。
[0160]
顯然,本領(lǐng)域的技術(shù)人員可以對(duì)本發(fā)明進(jìn)行各種改動(dòng)和變型而不脫離本發(fā)明的精神和范圍。這樣,倘若本發(fā)明的這些修改和變型屬于本發(fā)明權(quán)利要求及其等同技術(shù)的范圍
之內(nèi),則本發(fā)明也意圖包含這些改動(dòng)和變型在內(nèi)。
技術(shù)特征:
1.一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,其特征在于,包括以下步驟:(1)求解提升機(jī)主軸變形的徑向位移u
ρ
(x,y,z;t)、切向位移和軸向翹曲u
z
(x,y,z;t);(2)建立主軸段的三維cartesian坐標(biāo)系,根據(jù)建立的坐標(biāo)系,用步驟(1)求解的三個(gè)位移分量表示主軸段的位移場(chǎng);(3)引入carrera通用格式,根據(jù)一維梁理論,將步驟(2)的主軸位移場(chǎng)采用張量表示,然后基于二元級(jí)數(shù)展開,主軸上一點(diǎn)與z軸的垂直距離ρ在柱坐標(biāo)系下用矩陣形式表示廣義坐標(biāo)向量ψ;(4)根據(jù)經(jīng)典彈性力學(xué)理論,小位移變形情況下,由步驟3求出的主軸位移場(chǎng),在柱坐標(biāo)系下表示出線性微分算子c,由hooke定律求出應(yīng)力向量σ,計(jì)算本構(gòu)矩陣e;(5)根據(jù)虛位移原理,由應(yīng)變能公式、勢(shì)能公式和動(dòng)能公式計(jì)算出提升機(jī)主軸的應(yīng)變能、勢(shì)能和動(dòng)能,采用hamilton原理,得到相應(yīng)的控制微分方程;(6)運(yùn)用插值函數(shù),表示出節(jié)點(diǎn)的廣義位移d,帶入步驟(5)中的微分控制方程,化簡(jiǎn)得到最終結(jié)果;(7)根據(jù)步驟(1)-步驟(6),利用matlab求出提升機(jī)主軸的總體質(zhì)量矩陣和總體剛度矩陣,進(jìn)一步求解得到主軸的固有頻率,將該計(jì)算結(jié)果與ansys模擬得到的結(jié)果進(jìn)行對(duì)比,驗(yàn)證提升機(jī)主軸的動(dòng)力學(xué)建模方法的準(zhǔn)確性。2.如權(quán)利要求1所述的一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,其特征在于,所述步驟(2)中位移場(chǎng)為:u(x,y,z;t)=ψ
i
(x,z)u
i
(y;t)i=1,2,
…
,n;其中ψ
i
是廣義坐標(biāo)向量,是截面上坐標(biāo)x和z的函數(shù),u
i
是廣義位移向量,n是展開式項(xiàng)數(shù),下標(biāo)i表示張量疊加。3.如權(quán)利要求2所述的一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,其特征在于,所述廣義位移向量u
i
表示為:u
x
=u1+xu2+yu3+x2u4+xyu5+y2u6;u
y
=v1+xv2+yv3+x
2v4
+xyv5+y
2v6
;u
z
=w1+xw2+yw3+x2w4+xyw5+y2w6;根據(jù)極坐標(biāo)與直角坐標(biāo)的轉(zhuǎn)換為:其中x、y表示主軸截面的坐標(biāo),ρ、表示主軸在柱坐標(biāo)系下的坐標(biāo),u
x
、u
y
、u
z
表示主軸任意一點(diǎn)在直角坐標(biāo)系下三個(gè)方向的位移分量,u
ρ
、表示主軸在柱坐標(biāo)下ρ軸和軸的位移分量,u1~u6表示x軸方向的6個(gè)廣義位移,v1~v6表示y軸方向的6個(gè)廣義位移,w1~w6表示z軸方向的6個(gè)廣義位移。主軸廣義坐標(biāo)向量ψ
i
選用的是由n階基函數(shù)x
i
y
j
構(gòu)成的二元taylor多項(xiàng)式,當(dāng)下標(biāo)張量i=2時(shí),ψ=ψ2,其中ψ參數(shù)表示為:
其中:其中:其中:其中:其中:其中ψ表示下標(biāo)張量為2的廣義坐標(biāo)向量,ρ、表示主軸在柱坐標(biāo)系下的坐標(biāo)。4.如權(quán)利要求1所述的一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,其特征在于,步驟(4)中線性微分算子矩陣c表示為:根據(jù)hooke定律,應(yīng)力向量σ表示為:σ=eε;式中:;為應(yīng)變向量;其中ε表示應(yīng)變向量,ε
r
、ε
z
表示主軸在柱坐標(biāo)系下三個(gè)方向的線應(yīng)變,γ
rz
、表示主軸在柱坐標(biāo)系下的三個(gè)角應(yīng)變,c表示線性微分算子矩陣,u表示主軸在柱坐標(biāo)系下的位移場(chǎng);其中σ表示應(yīng)力向量,σ
r
、σ
z
表示主軸在柱坐標(biāo)系下三個(gè)方向的正應(yīng)力,σ
rz
、表示主軸在柱坐標(biāo)系下的三個(gè)切應(yīng)力;利用上述公式得出:本構(gòu)矩陣e為:λ和μ分別記為:其中λ和μ是lame常數(shù),e表示材料的彈性模量,ν表示材料的泊松比。5.如權(quán)利要求1所述的一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,其特征在于,步驟(5)中應(yīng)變能、勢(shì)能和動(dòng)能分別表示為u、u
p
和t,根據(jù)hamiltion原理,采用以下公式推導(dǎo)出相應(yīng)的控制微分方程:
其中λ是軸長(zhǎng)區(qū)間,α是截面面域,ω表示軸段截面,u是廣義位移向量,p是體分布力向量,q是表面分布力向量,z1,z2(z1<z2)是軸兩端的軸向坐標(biāo),是端面上應(yīng)力向量,()表示端面上的物理量,表示徑向應(yīng)力分量,表示軸向應(yīng)力分量,η表示材料密度,t表示主軸運(yùn)動(dòng)時(shí)間,r表示軸段半徑;根據(jù)hamiltion原理:l=t-u-u
p
;其中δ表示變分運(yùn)算,t表示運(yùn)動(dòng)時(shí)間,u表示主軸位移場(chǎng);導(dǎo)出控制微分方程為:6.如權(quán)利要求5所述的一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,其特征在于,步驟(6)中節(jié)點(diǎn)廣義位移和插值函數(shù)分別記為d和n,帶入控制微分方程并化簡(jiǎn)得到最終結(jié)果的過程如下;d是節(jié)點(diǎn)廣義位移;d={d
u1t d
v1t d
w1t d
u2t d
v2t d
w2t
}
t
;d
u(1)
={u
1(1)
?…?
u
6(1)
}
t
,d
v(1)
={v
1(1)
?…?v6(1)
}
t
,d
w(1)
={w
1(1)
?…?
w
6(1)
}
t
;d
u(2)
={u
1(2)
?…?
u
6(2)
}
t
,d
v(2)
={v
1(2)
?…?v6(2)
}
t
,d
w(2)
={w
1(2)
?…?
w
6(2)
}
t
;采用c0插值函數(shù):u=nd=[n
1 n2]d;]d;其中n是插值函數(shù),d是節(jié)點(diǎn)廣義位移,ξ是單元內(nèi)的自然坐標(biāo),其取值區(qū)間為[-1,1];
帶入控制微分方程并化簡(jiǎn)得:其中表示端面上的插值函數(shù),()表示端面上的物理量;整理為:整理為:整理為:整理為:其中jacobian函數(shù)j=l/2,l為軸段軸向長(zhǎng)度積分空間,m為質(zhì)量矩陣,k為剛度矩陣,f為邊界條件。
技術(shù)總結(jié)
本發(fā)明公開了一種基于級(jí)數(shù)展開的提升機(jī)主軸動(dòng)力學(xué)建模方法,包括以下步驟:(1)求解提升機(jī)主軸變形的徑向位移、切向位移和軸向翹曲;(2)求解的三個(gè)位移分量表示主軸段的位移場(chǎng);(3)將步驟(2)的主軸位移場(chǎng)采用張量表示,主軸上一點(diǎn)與z軸的垂直距離ρ在柱坐標(biāo)系下用矩陣形式表示廣義坐標(biāo)向量ψ;(4)在柱坐標(biāo)系下表示出線性微分算子C,由Hooke定律求出應(yīng)力向量σ,計(jì)算本構(gòu)矩陣E;(5)得到相應(yīng)的控制微分方程;(6)運(yùn)用插值函數(shù),表示出節(jié)點(diǎn)的廣義位移d,帶入步驟(5)中的微分控制方程,化簡(jiǎn)得到最終結(jié)果;(7)驗(yàn)證提升機(jī)主軸的動(dòng)力學(xué)建模方法的準(zhǔn)確性,具有更高的計(jì)算效率,適用范圍廣。適用范圍廣。適用范圍廣。