基于張量鏈分解的稀疏立方陣列波達方向估計方法
1.本發明屬于陣列信號處理技術領域,尤其涉及基于稀疏陣列虛擬域張量的統計信號處理技術,具體是一種基于張量鏈分解的稀疏立方陣列波達方向估計方法,可用于目標定位。
背景技術:
2.相比于傳統遵循奈奎斯特采樣速率的均勻陣列,稀疏陣列具有大孔徑、高分辨率的優勢,能夠突破傳統均勻陣列波達方向估計在估計性能與成本開銷上的性能瓶頸。具有系統化結構的稀疏陣列基于接收信號的二階統計量推導增廣虛擬陣列,從而基于虛擬域二階等價信號實現奈奎斯特匹配的波達方向估計。嵌套互質陣列作為一種典型的稀疏陣列架構,能夠推導出連續的虛擬陣列,因此得到廣泛應用。然而,傳統的虛擬域信號處理方法將接收信號表示成矢量,并通過矢量化接收信號的協方差矩陣推導虛擬域二階等價信號;隨著實際應用中稀疏陣列維度的不斷擴張,多維稀疏陣列的接收信號涵蓋多維度時空信息,而這種矢量化信號的處理方法將破壞多維接收信號的原始結構,造成嚴重的性能損失。
3.為了保留多維接收信號的結構化信息,張量作為一種多維的數據類型,開始被應用于陣列信號處理領域,用于表征涵蓋多維時空信息的接收信號。現有面向多維稀疏陣列的張量信號處理方法通過推導二階虛擬域張量,將對應的高維虛擬域協方差張量表示為canonical polyadic(cp)模型,對其進行直接canonical polyadic分解以實現高精度、高分辨的波達方向估計。然而,canonical polyadic分解在處理高維張量的時候,存在收斂速度慢、計算復雜度高的問題。而張量鏈分解作為另外一種張量分解形式,能夠將高維張量高效分解為若干低維度核張量和矩陣的鏈式連接形式,進而針對低維核張量做后續處理,能夠在保障計算效率的前提下有效提取信號特征,從而實現信道估計、諧波檢索、高光譜圖像去噪等具體功能。由此可見,張量鏈分解在提升稀疏陣列波達方向估計的處理效率方面具有極大潛力。針對高維虛擬域協方差張量,如何運用張量鏈分解設計一種低計算復雜度的波達方向估計方法仍是一個亟待解決的問題。
技術實現要素:
4.本發明的目的在于針對現有技術的不足,提供一種基于張量鏈分解的稀疏立方陣列波達方向估計方法。
5.本發明的目的是通過以下技術方案實現的:一種基于張量鏈分解的稀疏立方陣列波達方向估計方法,包含以下步驟:
6.(1)接收端使用m
xmymz
+n
x
nyn
z-1個物理天線陣元,按照三維嵌套互質立方陣列的結構進行架構;該嵌套互質立方陣列分解為一個均勻立方子陣列和一個稀疏立方子陣列其中包含m
x
×my
×mz
個天線陣元,陣元間距d為入射窄帶信號波長λ的一半,即d=λ/2,包含n
x
×
ny×
nz個天線陣元,在x軸方向、y軸方向和z軸方向上的間距分別為m
x
d、myd和mzd;
7.(2)假設有k個來自方向的遠場窄帶非相關信號源,θk和分別為第k個入射信號源的方位角和俯仰角,k=1,2,
…
,k,將嵌套互質立方陣列中均勻立方子陣列的t個采樣快拍信號在第四個維度進行疊加后,得到一個四維張量信號建模為:
[0008][0009]
其中,sk=[s
k,1
,s
k,2
,
…
,s
k,t
]
t
為對應第k個入射信號源的多快拍采樣信號波形向量,[
·
]
t
表示轉置操作,表示矢量外積,為與各信號源相互獨立的噪聲張量,和分別為在x軸、y軸和z軸方向上的導引矢量,表示為:
[0010][0011][0012][0013]
其中,
[0014]
稀疏立方子陣列的接收信號用四維張量信號表示為:
[0015][0016]
其中,為與各信號源相互獨立的噪聲張量,和分別為在x軸、y軸和z軸方向上的導引矢量,表示為:
[0017][0018][0019][0020]
通過求四維張量信號和的互相關統計量,得到二階互相關張量
[0021][0022]
其中,表示第k個入射信號源的功率,表示六維互相關噪聲張量,《
·
,
·
》r表示兩個張量沿著第r維度的張量縮并操作,e[
·
]表示取數學期望操作,(
·
)
*
表示共軛操作;這里,六維互相關噪聲張量的第(1,1,1,1,1,1)個元素取值為噪聲功率而其他元素取值均為0;
[0023]
(3)定義維度集合通過對互相關張量進行維度合并的張量變換,得到一個三維張量
[0024][0025]
其中,其中,通過在指數項上形成差集數組,構造出一個大小為m
xnx
×my
ny×mz
nz的虛擬均勻立方陣列的虛擬均勻立方陣列表示克羅內克積;噪聲張量的第(1,1,1)個元素取值為而其他元素取值均為0;將三維張量中的元素進行排列,以對應中虛擬陣元的位置,得到三維虛擬域張量
[0026][0027]
其中,
[0028]
和分別為虛擬均勻立方陣列沿x軸、y軸和z軸上的導引矢量,噪聲張量的第(m
xnx-m
x
+1,myn
y-my+1,mzn
z-mz+1)個元素取值為而其他元素取值均為0;
[0029]
(4)計算對應于虛擬域張量的虛擬域協方差張量的虛擬域協方差張量表示為如下canonical polyadic模型:
[0030]
[0031]
其中,對角張量的對角線元素為b
x
==為canonical polyadic因子矩陣,為噪聲張量,
×i表示沿著第i維度的張量-矩陣內積;
[0032]
(5)通過張量鏈分解,將虛擬域協方差張量表示為矩陣與三維核張量的鏈式連接形式,即:
[0033][0034]
其中,為首矩陣,為首矩陣,為四個三維核張量,為尾矩陣,表示沿著張量第r1維度與張量第r2維度的張量縮并操作;
[0035]
(6)對核張量進行canonical polyadic分解,表示為:
[0036][0037]
其中,對角張量的對角線元素為幅度因子[λ1,λ2,
…
,λk],為對應虛擬域協方差張量第一和第二維度的基變換矩陣,為canonical polyadic因子矩陣by的估計值;由此,的第一個canonical polyadic因子矩陣b
x
通過張量鏈首矩陣g1的基變換估計得到,即:
[0038][0039]
其中(
·
)-1
表示矩陣求逆操作;從估計的canonical polyadic因子矩陣和中提取角度信息,得到二維波達方向估計結果
[0040]
進一步地,步驟(1)所述的三維嵌套互質立方陣列結構具體描述為:均勻立方子陣列中天線陣元在三維坐標系上的位置坐標為{(m
x
d,myd,mzd)|m
x
=0,1,
…
,m
x-1,my=0,1,
…
,m
y-1,mz=0,1,
…
,m
z-1};稀疏立方子陣列中天線陣元在三維坐標系上的位置坐標為{(n
xmx
d,n
ymy
d,n
zmz
d)|n
x
=0,1,
…
,n
x-1,ny=0,1,
…
,n
y-1,nz=0,1,
…
,n
z-1};{m
x
,n
x
}、{my,ny}、{mz,nz}分別為一對互質整數;將和按照坐標系原點位置陣元重疊的方式進行子陣列組合,由于和的陣元排布滿足互質數條件,因此除坐標系原點位置以外的其余位置陣元均不重疊,獲得實際包含m
xmymz
+n
x
nyn
z-1個天線陣元的嵌套互質立方陣列。
[0041]
進一步地,步驟(2)所述的二階互相關張量推導,在實際中,通過計算四維張量信號和的采樣互相關統計量近似得到,即采樣互相關張量
[0042]
[0043]
進一步地,步驟(5)中,虛擬域協方差張量的張量鏈分解按如下步驟進行計算:沿著第一維度對進行展開,得到對進行截斷奇異值分解:
[0044][0045]
其中,為奇異值矩陣,為右奇異值矩陣;將重構為一個輔助矩陣其中reshape{
·
}表示將一個矩陣按指定維度大小重構為另一矩陣或張量的操作;通過對c1使用截斷奇異值分解得到:
[0046]
c1=u2λ
2v2
,
[0047]
其中,為左奇異值矩陣,為奇異值矩陣,為奇異值矩陣,為右奇異值矩陣,通過重構u2得到核張量即重復上述步驟,核張量和尾矩陣g6利用左奇異值矩陣{ur,r=3,4,5,6}依次對應生成。
[0048]
進一步地,步驟(6)中,從估計的canonical polyadic因子矩陣和中提取參數μk和vk,表示為:
[0049][0050][0051]
其中,與分別表示的第m行元素與的第n行元素,∠(
·
)表示對一個復數取幅角操作;基于(μk,vk)與二維波達方向的對應關系,得到二維波達方向估計的閉式解為:
[0052][0053][0054]
本發明的有益效果是:本發明主要解決現有方法中通過canonical polyadic(cp)分解直接處理高維虛擬域協方差張量時計算復雜度高的問題,其實現步驟是:構建三維嵌套互質立方陣列;嵌套互質立方陣列接收信號的張量建模;通過互相關張量變換構造對應于虛擬均勻立方陣列的虛擬域張量;推導虛擬域協方差張量;對虛擬域協方差張量進行張
量鏈分解;從張量鏈首矩陣和核張量中提取cp因子矩陣并獲取波達方向估計結果。本發明通過張量鏈分解對高維虛擬域協方差張量進行降維表征,進而從低維度矩陣和核張量中高效提取角度信息,實現了低復雜度、高精度的波達方向估計,可用于目標定位。
附圖說明
[0055]
圖1是本發明的總體流程框圖。
[0056]
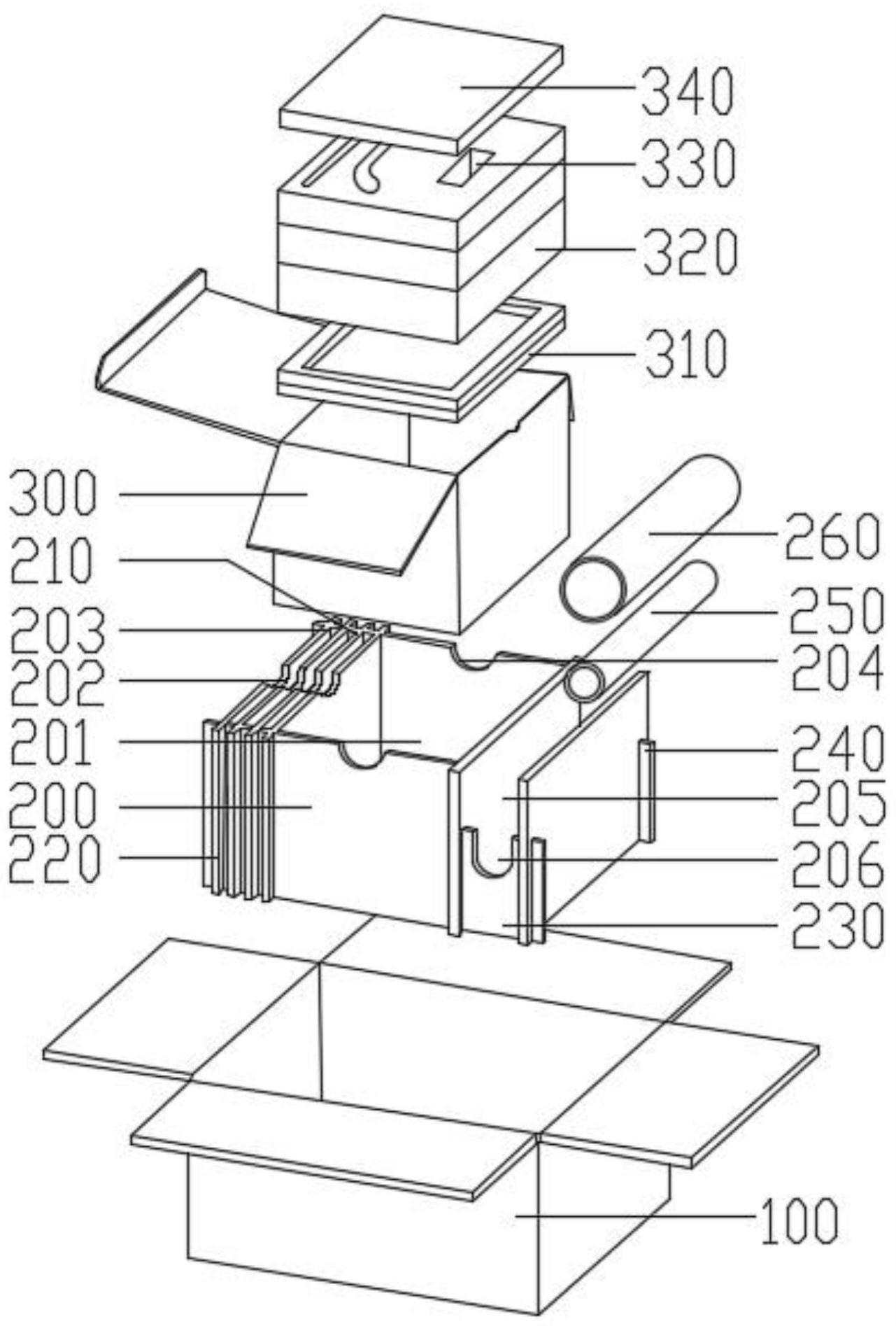
圖2是本發明所構建的嵌套互質立方陣列結構示意圖。
[0057]
圖3是本發明所提方法在不同信噪比條件下的波達方向估計精度性能比較圖。
[0058]
圖4是本發明所提方法在不同采樣快拍數條件下的波達方向估計精度性能比較圖。
[0059]
圖5是本發明所提方法在不同信噪比條件下的運行時間比較圖。
[0060]
圖6是本發明所提方法在不同采樣快拍數條件下的運行時間比較圖。
具體實施方式
[0061]
以下參照附圖,對本發明的技術方案作進一步的詳細說明。
[0062]
為了解決現有方法通過canonical polyadic分解直接處理高維虛擬域協方差張量時計算復雜度高的問題,本發明提出了一種基于張量鏈分解的稀疏立方陣列波達方向估計方法,通過對虛擬域協方差張量進行張量鏈分解,從降維張量鏈首矩陣和核張量中提取canonical polyadic因子矩陣,實現高效的波達方向估計。參照圖1,本發明的實現步驟如下:
[0063]
步驟1:構建三維嵌套互質立方陣列。接收端使用m
xmymz
+n
x
nyn
z-1個物理天線陣元,按照三維嵌套互質立方陣列的結構進行架構,如圖2所示,該嵌套互質立方陣列分解為一個均勻立方子陣列和一個稀疏立方子陣列其中包含m
x
×my
×mz
個天線陣元,陣元間距d為入射窄帶信號波長λ的一半,即d=λ/2,中天線陣元在三維坐標系上的位置坐標為{(m
x
d,myd,mzd)|m
x
=0,1,
…
,m
x-1,my=0,1,
…
,m
y-1,mz=0,1,
…
,m
z-1};包含n
x
×
ny×
nz個天線陣元,這些天線陣元在x軸方向、y軸方向和z軸方向上的間距分別為m
x
d、myd和mzd,在三維坐標系上的位置坐標為{(n
xmx
d,n
ymy
d,n
zmz
d)|n
x
=0,1,
…
,n
x-1,ny=0,1,
…
,n
y-1,nz=0,1,
…
,n
z-1};{m
x
,n
x
}、{my,ny}、{mz,nz}分別為一對互質整數;將和按照坐標系原點位置陣元重疊的方式進行子陣列組合,由于和的陣元排布滿足互質數條件,因此除坐標系原點位置以外的其余位置陣元均不重疊,獲得實際包含m
xmymz
+n
x
nyn
z-1個天線陣元的嵌套互質立方陣列;
[0064]
步驟2:嵌套互質立方陣列接收信號的張量建模。假設有k個來自方向的遠場窄帶非相關信號源,θk和分別為第k個入射信號源的方位角和俯仰角,k=1,2,
…
,k,將嵌套互質立方陣列中均勻立方子陣列的t個采樣快拍信號在第四個維度進行疊加后,可以得到一個四維張量信號建模為:
[0065][0066]
其中,sk=[s
k,1
,s
k,2
,
…
,s
k,t
]
t
為對應第k個入射信號源的多快拍采樣信號波形向量,[
·
]
t
表示轉置操作,表示矢量外積,為與各信號源相互獨立的噪聲張量,和分別為在x軸、y軸和z軸方向上的導引矢量,表示為:
[0067][0068][0069][0070]
其中,
[0071]
類似地,稀疏立方子陣列的接收信號可以用四維張量信號的接收信號可以用四維張量信號表示為:
[0072][0073]
其中,為與各信號源相互獨立的噪聲張量,和分別為在x軸、y軸和z軸方向上的導引矢量,表示為:
[0074][0075][0076][0077]
通過求四維張量信號和的互相關統計量,得到二階互相關張量
[0078][0079]
其中,表示第k個入射信號源的功率,表示六維互相關噪聲張量,《
·
,
·
》r表示兩個張量沿著第r維度的張量縮并操作,e[
·
]表
示取數學期望操作,(
·
)
*
表示共軛操作。這里,六維互相關噪聲張量的第(1,1,1,1,1,1)個元素取值為噪聲功率而其他元素取值均為0。在實際中,通過計算張量信號和的采樣互相關統計量近似得到,即采樣互相關張量
[0080][0081]
步驟3:通過互相關張量變換構造對應于虛擬均勻立方陣列的虛擬域張量。由于互相關張量中包含了均勻立方子陣列和稀疏立方子陣列的空間信息,通過合并中表征同一方向空間信息的維度,可以使兩個子陣列對應相同方向的導引矢量在指數項上形成差集數組,從而構造三維的虛擬均勻立方陣列。具體地,互相關張量的第1、4維度表征x軸方向的空間信息,第2、5維度表征y軸方向的空間信息,第3、6維度表征z軸方向的空間信息;為此,定義維度集合通過對互相關張量進行維度合并的張量變換,得到一個三維張量
[0082][0083]
其中,其中,通過在指數項上形成差集數組,構造出一個大小為m
xnx
×my
ny×mz
nz的虛擬均勻立方陣列的虛擬均勻立方陣列表示kronecker積。噪聲張量的第(1,1,1)個元素取值為而其他元素取值均為0。將三維張量中的元素進行排列,以對應中虛擬陣元的位置,即可得到三維虛擬域張量得到三維虛擬域張量
[0084][0085]
其中,其中,和分別為虛擬均勻立方陣列沿x軸、y軸和z軸上的導引矢量,噪聲張量的第(m
xnx-m
x
+1,myn
y-my+1,mzn
z-mz+1)個元素取值為而其他元素取值均為0;
[0086]
步驟4:推導虛擬域協方差張量。計算對應于虛擬域張量的虛擬域協方差張量表示為如下canonicalpolyadic模型:
[0087][0088]
其中,對角張量的對角線元素為的對角線元素為的對角線元素為的對角線元素為為canonical polyadic因子矩陣,為噪聲張量,
×i表示沿著第i維度的張量-矩陣內積;
[0089]
步驟5:對虛擬域協方差張量進行張量鏈分解。為了確保對虛擬域協方差張量中的canonical polyadic因子進行高效提取,不同于傳統方法對其直接進行canonical polyadic分解的操作,通過張量鏈分解對其進行降維處理。具體而言,將虛擬域協方差張量表示為矩陣與三維核張量的鏈式連接形式,即:
[0090][0091]
其中,為首矩陣,為首矩陣,為四個三維核張量,為尾矩陣,表示沿著張量第r1維度與張量第r2維度的張量縮并操作。上述虛擬域協方差張量的張量鏈分解可按如下步驟進行計算:沿著第一維度對進行展開,得到進而對進行截斷奇異值分解(truncated singular value decomposition):
[0092][0093]
其中,為奇異值矩陣,為右奇異值矩陣。將重構為一個輔助矩陣其中reshape{
·
}表示將一個矩陣按指定維度大小重構為另一矩陣或張量的操作。通過對c1使用截斷奇異值分解可得到:
[0094]
c1=u2λ
2v2
,
[0095]
其中,為左奇異值矩陣,為奇異值矩陣,為奇異值矩陣,為右奇異值矩陣,通過重構u2可得到核張量即重復上述步驟,核張量和尾矩陣g6可利用左奇異值矩陣{ur,r=3,4,5,6}依次對應生成;
[0096]
步驟6:從張量鏈首矩陣和核張量中提取cp因子矩陣并獲取波達方向估計結果。由于canonical polyadic因子矩陣b
x
與by可用于估計信號源的二維波達方向,因此將虛擬域協方差張量通過張量鏈分解得到的首矩陣g1和核張量轉換為b
x
與by。具體過程為:對核張量進行canonical polyadic分解,表示為:
[0097][0098]
其中,對角張量的對角線元素為幅度因子[λ1,λ2,
…
,λk],為對應虛擬域協方差張量第一和第二維度的基變換矩陣,為canonical polyadic因子矩陣by的估計值。由此,的第一個canonical polyadic因子矩陣b
x
可以通過張量鏈首矩陣g1的基變換得到,即:
[0099][0100]
其中(
·
)-1
表示矩陣求逆操作。進而,從和中估計μk和νk,表示為:
[0101][0102][0103]
其中,與分別表示的第m行元素與的第n行元素,∠(
·
)表示對一個復數取幅角操作。基于(μk,vk)與二維波達方向的對應關系,得到二維波達方向估計的閉式解為:
[0104][0105][0106]
下面結合仿真實例對本發明的效果做進一步的描述。
[0107]
仿真實例:采用嵌套互質立方陣列接收入射信號,其參數選取為m
x
=my=mz=3,n
x
=ny=nz=4,即架構的嵌套互質立方陣列共包含m
xmymz
+n
x
nyn
z-1=90個物理陣元。所構造的虛擬均勻立方陣列共有12
×
12
×
12個虛擬陣元。將本發明所提基于張量鏈分解的稀疏立方陣列波達方向估計方法與傳統基于canonical polyadic分解的方法和基于旋轉不變子空間(estimating signal parameter via rotational invariance techniques,esprit)的方法進行對比。假定有2個入射信號,每次試驗的信號方位角和俯仰角均在[15
°
,60
°
]范圍內隨機生成。在采樣快拍數t=150的條件下,繪制均方根誤差(root-mean-square error,rmse)隨信噪比(signal-to-noise ratio,snr)變化的性能對比曲線,如圖3所示;在信噪比snr=-5db的條件下,繪制rmse隨采樣快拍數t變化的性能對比曲線,如圖4所示。進一步地,對比上述方法的計算效率,繪制計算機運行時間隨snr變化的對比曲線,如圖5所示;并繪制計算機運行時間隨采樣快拍數t的對比曲線,如圖6所示。從對比結果看出,相比于傳統基于esprit的方法,本發明所提方法通過構建虛擬域張量,充分利用所對應高維虛擬域協方差
張量的結構化信息,具備更優的波達方向估計性能,且基于張量鏈分解對虛擬域協方差張量進行高效特征提取,具備更短的運行時間;相比基于canonical polyadic分解的方法,本發明所提方法在虛擬域協方差張量的張量鏈分解過程中最大程度降低信息損失,不僅表現出更高的估計精度,還使得計算復雜度大幅度降低,顯著提升了計算效率。
[0108]
綜上所述,本發明通過對高維虛擬域協方差張量進行張量鏈分解,并設計了相應canonical polyadic因子的高效提取策略,實現了低復雜度、高精度的稀疏立方陣列波達方向估計。
[0109]
以上所述僅是本發明的優選實施方式,雖然本發明已以較佳實施例披露如上,然而并非用以限定本發明。任何熟悉本領域的技術人員,在不脫離本發明技術方案范圍情況下,都可利用上述揭示的方法和技術內容對本發明技術方案做出許多可能的變動和修飾,或修改為等同變化的等效實施例。因此,凡是未脫離本發明技術方案的內容,依據本發明的技術實質對以上實施例所做的任何的簡單修改、等同變化及修飾,均仍屬于本發明技術方案保護的范圍內。