一種基于FETI的高精細流致振動模擬方法
一種基于feti的高精細流致振動模擬方法
技術領域
1.本發明屬于反應堆流致振動數值模擬實現領域,具體涉及一種基于feti的大規模流致振動高精度模擬方法。
背景技術:
2.反應堆堆芯組件具有多樣性和復雜性,全堆高精細結構力學模擬所需的計算資源和存儲在小型集計算系統中難以實現。依托高性能計算技術來實現高精細的數值計算就成為研究反應堆安全性的必要途徑,依托超級計算機,采用數學物理計算方法,對反應堆堆中子物理、結構力學、燃料性能等物理過程進行精細化數值模擬,已成為國際上一個前沿研究熱點。
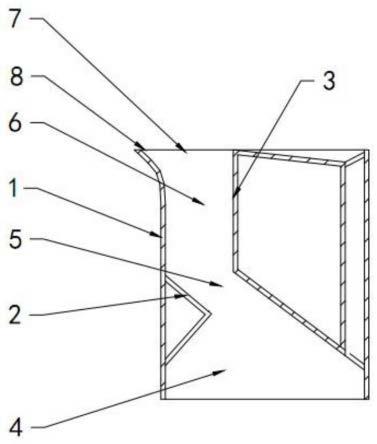
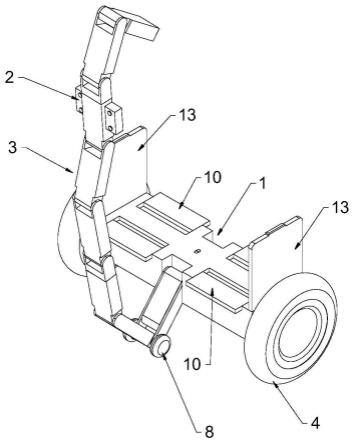
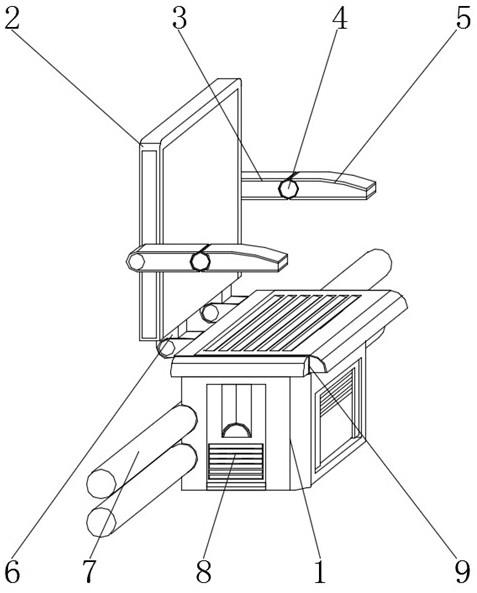
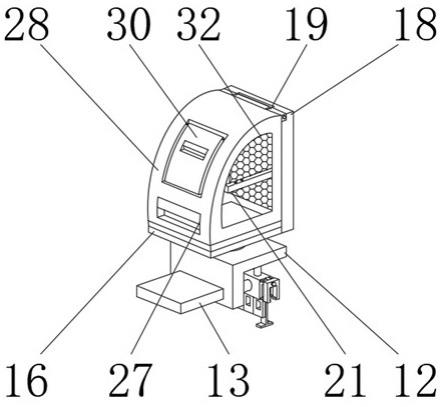
3.燃料棒組件在高溫、高壓以及強輻照下運行,并且長期承受冷卻劑的沖刷。冷卻劑的循環流動會引起燃料棒組件的長期微幅振動,且總是伴隨著反應堆的運行而存在,這些振動使燃料棒在與格架接觸的界面上產生相對位移,并在支撐處發生包殼磨損(grid-to-rod fretting,gtrf)。燃料棒的這種漸進磨損是影響燃料組件在正常運行和事故工況下結構完整性的關鍵因素,根據全世界燃料棒失效率的統計數據,gtrf磨損失效事故占比高達78%。為確保結構在使用壽命期內的完整性,只能通過優化結構設計和調整流速,將流致振動引起的結構振動響應控制在可接受的范圍之內。因此,燃料組件流致振動數值分析與計算是安全分析不可缺少的重要內容。
4.高精細的分析和模擬燃料棒的流致振動,如對于第四代快堆帶繞絲的燃料棒的高精度數值模擬,往往需要生成千萬單元以上規模的網格數據。考慮湍流模型時所需網格規模更是達到了數億乃至上十億網格節點,這對計算機的硬件配置、計算算法及其前處理過程的時空效率都提出了嚴峻的挑戰。使用串行算法求解問題,在內存空間和時間上都變的不可接受。以開源軟件code_aster為例,僅對一螺距單根帶繞絲燃料棒(約為10萬網格單元)的流致振動模擬采用單核求解,其用時需達2小時。以此估算,針對億量級單元的串行求解,在內存空間和時間上都變的不可接受。當前的研究大多針對小規模算例,并未對千萬單元以上規模算例進行分析。利用高性能計算機,開發高效并行的多領域數值模擬求解算法及與之對應的并行前后處理算法是迎接這一挑戰的必由之路。開展流致振動并行求解方法研究,是提高流致振動求解效率的關鍵所在。
5.有限元法是求解復雜工程問題的一種近似數值解法,現已廣泛應用到力學、熱學、電磁學等各個學科。傳統的有限元法一般以串行的方式進行求解,稱為串行有限元法。串行有限元法在面對大型復雜工程問題時,往往會出現求解時間過長、內存占用過高等現象。隨著支持并行計算的并行計算機問世,出現適用于將串行有限元法并行化的三種技術,分別是方程組并行求解、ebe(element-by-element)有限元法以及有限元區域分解法。基于舒爾補(schur complement)的有限元區域分解法,最早是由farhat等人提出,稱為撕裂有限元法(finite element tearing and interconnecting method,feti),常用于求解線性工程問題中出現的大型線性系統的數值解。在feti方法中,將一個主體分解為幾個不重疊的子
域,并且這些子域之間的連續性由拉格朗日乘數強制執行。feti方法使用對偶理論,可以導出較小且條件相對較好的對偶問題,并通過共軛梯度算法的合適變體有效解決。
技術實現要素:
6.為了解決上述問題,本發明提出了一種基于feti的高精細流致振動模擬方法。本發明涉及基于feti方法的newmark積分法模擬高精細流致振動和適用于feti方法的域邊界平衡的圖二分算法,feti方法的newmark積分法求解高精細流致振動問題過程分成兩個階段:第一階段大規模并行的feti方法被用于將上億網格單元的求解域劃分為多個非重疊求解子域進行并行求解;第二階段動力學newmark方法用于實現流致振動過程的時間步更新。
7.本發明方法的具體步驟是:
8.步驟1.讀入相應的算例數據,主要以網格數據為主,以及材料參數等。
9.步驟2.采用newmark方法對流致振動動力學過程進行數值離散。
10.步驟3.采用feti方法對離散后的方程進行并行分解,劃分子域,子域在劃分邊界處由拉格朗日乘子λ進行粘合,并滿足相應邊界條件。根據feti劃分子域邊界特點,提出了域邊界平衡的圖二分算法,均衡各個子域中的單元量和計算量,保證進程間負載均衡。
11.步驟4.采用預處理共軛梯度法進行迭代求解,迭代求解得到拉格朗日乘子λ。根據拉格朗日乘子λ得到相應的位移,記錄位移值。
12.步驟5.根據位移值,newmark方法實現流致振動過程的時間步更新。
13.本發明有益效果:本發明采用feti方法與newmark積分法相結合,完成了數億規模的網格數據求解,提高了求解大規模流致振動問題的效率,實現了流致振動的快速高效模擬。采用基于域邊界平衡的圖二分算法進行區域分解,保證了進程間的負載均衡,進一步提高了求解大規模流致振動問題的效率。
附圖說明
14.圖1是基于feti方法的newmark積分法求解高精細流致振動問題具體流程;
15.圖2是halo權重說明;
16.圖3是單次迭代求解時間比例;
17.圖4是多線程并行操作求解矩陣向量乘;
18.圖5是弱可擴展性測試。
具體實施方式
19.以下結合附圖對本發明作進一步說明,請參閱圖1;圖1給出了本發明求解高精細流致振動問題具體流程。主要分成兩個階段:第一階段為feti求解階段,該階段主要可以分成兩個步驟,第一步為采用域邊界平衡的圖二分算法進行子域劃分;第二步為采用預處理共軛梯度法進行迭代求解。第二階段為newmark方法進行時間步的更新。
20.下面分別對上述實施步驟進行詳細說明:
21.步驟1:采用cefr單盒燃料棒組件為例進行數值模擬。燃料棒束底部固支,模擬以流體壓力的形式作用在燃料棒和繞絲的外表面上。分布式讀取相應網格參數,網格文件格式為vtk格式,以四面體網格和六面體網格為主。設置需要讀入的相應材料參數,主要為材
料密度、彈性模量、泊松比、時間步長、劃分子域數等。此次模擬材料密度為7890kg/m3、泊松比為0.3、彈性模量為2.1*105mpa,模擬12個時間步長,每個時間步長為0.01秒,劃分子域數為512個子域。
22.步驟2:流致振動問題通過對平衡方程、質量矩陣、阻尼矩陣、幾何方程、物理方程和位移邊界條件采用虛功原理推導得到整體動力方程,用數值算法(newmark算法)根據當前時刻及前幾個時刻體系的動力反應值來建立下一時刻的動力反應方程,并進行求解,針對燃料棒流致振動問題建模得到下面的整體動力方程:
[0023][0024]
其中,m為質量矩陣,c為阻尼矩陣,k為剛度矩陣,f(t)是節點載荷,u為求解的燃料棒的位移向量,u的一階導數為速度,u的二階導數為加速度。采用newmark方法對該動力學過程進行數值離散,newmark方法針對線性加速度假定做修正,在δ
t
+t時刻的速度和位移表達式中引入兩個參數η和γ得到newmark算法的離散格式:
[0025][0026][0027]
將(2)式與(3)式代入原始二階微分方程(1)式中,可得:
[0028][0029]
將(4)式簡化為下面關于求解未知量u
n+1
的線性方程形式,n為時間:
[0030]
au
n+1
=hn????????
(5)
[0031]
其中矩陣a和矩陣hn分別為
[0032][0033][0034]
步驟3:采用feti方法對離散后的方程進行并行分解,劃分子域。在feti方法進行子域劃分時,采用本發明提出的基于域邊界平衡的圖二分算法對求解域進行子域劃分,將求解域分解為i個獨立的非重疊子域,這些子域在劃分邊界處由拉格朗日乘子λ進行粘合,并滿足邊界條件。這樣公式5可轉化成如下形式:
[0035][0036]
其中,
[0037][0038]
表示分解后的各子域位移向量,bi為一個有符號布爾矩陣,定義子域與相鄰子域的連通性,由1、-1和0組成。如果子域x、y連通,設置子域x到子域y的系數為1,子域y到子域x的系數為-1;如果子域x、y不連通,設置系數為0。o為零矩陣。
[0039]
feti方法特殊的邊界處理方式,會使得傳統的點分割方法產生嚴重的邊劃分不均衡現象以及邊的缺失。子域邊界的節點數量影響著迭代求解效率,構建的求解矩陣計算成本隨著邊的計算成本的增加而增加。因此,保證每個子域邊界的節點數量均衡至關重要。在feti的區域分解時,采用基于域邊界平衡的圖二分算法不僅可以保證各個子域內部節點均衡,還能確保這個子域邊界節點均衡,從而提高了對應的求解效率。
[0040]
在傳統的貪心圖增長算法基礎上,對頂點增加兩個權重:對屬于邊界節點的頂點設置halo權重為1,非邊界節點的頂點設置halo權重為0,對子圖內部非邊界節點的頂點設置halo權重為1,屬于邊界節點的頂點設置halo權重為0。將halo權重為1的頂點添加至halo點集vh。請參閱圖2,左圖黑點為分隔符,將初始圖劃分兩張子圖,halo權重都為4。右圖為兩張子圖劃分為4張子圖,子圖的halo權重為別為4,4,4,4。
[0041]
如下偽代碼給出了域邊界平衡的圖二分算法具體流程:
[0042][0043]
首先在halo點集vh中選擇兩個種子頂點ω1和ω2,使得ω1與ω2盡可能保持距離,
以保證ω1與ω2,節點增長較晚的相遇。將初始圖劃分為兩張子圖,兩張子圖的點集分別用p1和p2表示。p1和p2最初為空,由種子頂點ω1和ω2生長出來。從ω1和ω2出發分別對剩下頂點做劃分,根據p1和p2兩個點集中的halo平衡情況進行調節。如果p1(或p2)中的halo權重為1的頂點比p2(或p1)中少,則盡可能選擇halo權重為1的目標頂點加入p1(或p2)。如果具有更多的halo權重為1的頂點,則優先選擇非halo權重為1的頂點加入p1(或p2)。考慮完halo平衡后,則p1選取離ω1最近和ω2最遠的頂點(dist(v,ω1)-dist(v,ω2)最小值的頂點)。這個過程需要滿足以下公式:
[0044][0045][0046]
其中s代表邊分隔符,vh代表求解域中的halo點集。保持最小的邊分隔符和halo節點均衡可以保證子域邊界的節點均衡以及各子域之間邊的負載均衡。選擇不同的種子頂點進行多次增長,根據最小邊分隔符和halo節點均衡進行分割。
[0047]
如表1、表2、表3所示可以發現采用本發明提出的基于域邊界平衡的圖二分算法與開源軟件metis的對比。表1對單元總數為29026600的六面體網格進行劃分。表中avg值為理想條件下的劃分數,max、min分別代表子域中網格最大數與網格最小數。從表1中可以看出來,本發明提出的方法劃分的最大最小子域數更接近理想值。表2對單元總數為102853760的四面體網格進行劃分同樣證明了本發明提出的方法進行子域劃分效果明顯較好。本方法對四面體網格算例劃分成512、256、128個子域用時與開源圖劃分軟件metis用時對比,兩者用時較為接近,子域劃分效率接近。
[0048]
表1六面體網格算例子域劃分對比
[0049][0050]
表2四面體網格算例子域劃分對比
[0051][0052]
表3子域劃分效率對比
[0053][0054]
步驟4:矩陣a和矩陣b均為非奇異矩陣,使得未知量λ具有唯一解。根據矩陣廣義逆得:
[0055]un+1
=a
+
(h
n-b
t
λ)+rα s.t.ar=o or r
t
a=o
???????????????
(12)
[0056]
其中,矩陣r為矩陣a零空間的基,a
+
是a的偽逆矩陣。將邊界條件bu=0代入至(12)式中可得:
[0057][0058]
這樣,原問題轉化為對關于未知量λ,α的方程組(13)的數值求解。這里采用預處理共軛梯度法對(13)式進行迭代求解。首先引入預處理矩陣p,對(13)式的第一個式子兩邊同時左乘矩陣p,用于消除α。從而得到(14)式:
[0059][0060]
其中,
[0061]
p=i-g(g
t
g)-1gt
?????????????????????????????
(15)
[0062]
對(14)式采用迭代求解得到λ,再代回(11)式解出α。將λ和α代入(12)式,得到每個求解域的當前時間步的位移向量,保存當前時間步計算結果u
n+1
。
[0063]
請參閱圖3,圖3給出了單次迭代求解時間比例。程序的計算時間主要由程序的迭代次數和單次迭代時間決定。在迭代求解過程中矩陣求解計算時間占到單次迭代時間的95%。每輪迭代都會執行以下步驟:投影、計算beta、矩陣向量乘、計算alpha、更新結果向量、更新殘差向量以及迭代數與迭代精度的判斷。
[0064]
基于feti方法求解流致振動算法流程的偽代碼如下:
[0065][0066]
偽代碼中8-10行為預處理共軛梯度法的迭代求解過程的投影步驟,投影存在大量的矩陣向量乘操作。在各個子域中計算ak、λk以及rk,需要先計算矩陣向量操作f
pk
。矩陣向量乘相互獨立,可以進行并行處理。可以將偽代碼中的8-10步與17步移植至國產加速器中來提高求解效率。針對曙光先進計算平臺架構(具體實驗環境如表4),對矩陣向量乘部分進行了異構移植,采用hip并行編程模型將具有較高計算密度的稠密矩陣向量乘計算交由國產加速器和cpu共同完成。采用openmp并行編程模型進行多線程并行操作。圖4給出了多線程并行操作求解矩陣向量乘的過程,一個線程用于控制國產加速器,調用rocblas線性代數庫進行稠密矩陣計算。利用線程調用hipmalloc函數,申請顯存空間,將存儲在cpu上的數據通過hipmemcpy傳遞給國產加速器顯存,通過調用hiplaunchkernel函數啟動核函數,再調用hipblas線性代數庫進行稠密矩陣計算。在國產加速器上的計算完成后再用hipmemcpy將結果傳遞給cpu,等待所有設備完成計算,同步數據,再進入下一次迭代。其他線程控制cpu核心,通過調用intel mkl數學庫計算剩余稠密矩陣向量。在迭代過程中,為了避免cpu與國產加速器之間頻繁數據交互帶來的時間開銷,在求解開始前就將所有稠密矩陣都傳遞至國產加速器中。在求解過程中,cpu與國產加速器根據各自任務的編排執行對應任務。
[0067]
表4實驗環境
[0068][0069]
在多個計算節點并行計算時,國產加速器需要從內存中讀取數據到顯存中,在計算結束后,需要將計算結果寫入內存。隨著問題規模變大,這樣的訪存操作時間開銷會逐漸增大。為充分利用國產加速器計算性能,本發明利用內存和顯存之間的雙緩沖技術,來減少訪存的時間。此外,為合理利用國產加速器顯存,采用數據對齊方法以減少顯存的不必要占用。在對齊邊界中創建數據,確保緩存線大小與向量數據對齊,避免編譯器額外計算,從而導致性能的損失。并利用內存合并訪問技術,獲取更高的吞吐量,以提高計算性能。
[0070]
步驟5:根據迭代求解得出的下一時間步的位移值代入(7)式更新hn,從而進入下一個時間步求解。newmark方法的計算精度取決于時間步長δt的大小。
[0071]
重復上述步驟2至步驟5直至達到所設定的時間步長數(注:域邊界平衡的圖二分算法在第一個時間步長劃分,后續不進行劃分)。如圖5所示,本發明在曙光先進計算平臺架構測試,計算量從0.48億擴展到7.6億,計算節點從128個擴展到2048個,每個節點處理64個子域,并行效率達到54%,可以明顯發現本發明具有良好的可擴展性,求解時間都在分鐘級別,具體實驗數據見表5所示。
[0072]
表5弱可擴展性實驗
[0073]