一種基于恢復(fù)型后驗誤差估計的網(wǎng)格自適應(yīng)方法
1.本發(fā)明屬于電磁場數(shù)值求解領(lǐng)域,具體為一種基于恢復(fù)型后驗誤差估計的網(wǎng)格自適應(yīng)方法。
背景技術(shù):
2.隨著計算機技術(shù)的發(fā)展,采用仿真技術(shù)對微波元器件的電磁場分布進行預(yù)先分析,是一種經(jīng)濟而有效的手段,因此在設(shè)計階段采用電磁仿真軟件對微波元器件電磁特性進行仿真計算是產(chǎn)品周期中必不可少的步驟。而對于計算機仿真來說,求解精度是一項備受關(guān)注的問題,提高求解精度也是計算機仿真的重要發(fā)展方向。對于有限元法來說,通常,模型離散的網(wǎng)格尺寸越小,仿真計算結(jié)果就越準(zhǔn)確。但是,如果只憑經(jīng)驗進行對某些計算區(qū)域進行網(wǎng)格加密,這是缺乏科學(xué)依據(jù)的,會帶來很多不確定的結(jié)果。因此,網(wǎng)格自適應(yīng)加密被提出來解決這一問題,通過得到的后驗誤差估計指示子,對當(dāng)前網(wǎng)格實施細化加密或粗化調(diào)整,進而給出下一步計算的網(wǎng)格,并通過自適應(yīng)誤差判斷結(jié)果是否收斂。
3.后驗誤差估計是自適應(yīng)的一個重要步驟。在誤差估計時,因為解析解是未知的,因此不能直接利用結(jié)果進行誤差計算,需要通過其它手段進行誤差估計。恢復(fù)型后驗誤差估計方法就是一種常用的方法。該方法首先構(gòu)造一種恢復(fù)解來代替解析解,然后構(gòu)造某種單元范數(shù)作為誤差的度量,利用這種范數(shù)獲得網(wǎng)格加密指示,然后進行網(wǎng)格加密。
4.恢復(fù)型后驗誤差估計方法的核心是恢復(fù)解的構(gòu)造。傳統(tǒng)的恢復(fù)解構(gòu)造方法,如基于超收斂特性的拼片修復(fù)法spr及其改進算法,存在計算量大、處理復(fù)雜、在邊界上需要特殊處理等問題。因此,需要構(gòu)造一種計算量較小、構(gòu)造簡單、具有普適性的恢復(fù)解用于后驗誤差估計,實現(xiàn)網(wǎng)格自適應(yīng)加密。
技術(shù)實現(xiàn)要素:
5.針對上述存在的問題,為解決現(xiàn)有網(wǎng)格自適應(yīng)加密由于恢復(fù)解構(gòu)造導(dǎo)致計算量大、處理復(fù)雜、普適性不高(在邊界上需要特殊處理)等問題,本發(fā)明提供了一種基于恢復(fù)型后驗誤差估計的網(wǎng)格自適應(yīng)方法,利用最小二乘原理構(gòu)造恢復(fù)解,完成后驗誤差估計,實現(xiàn)網(wǎng)格自適應(yīng)加密。
6.一種基于恢復(fù)型后驗誤差估計的網(wǎng)格自適應(yīng)方法,包括以下步驟:
7.a.將目標(biāo)微波元器件進行有限元建模,引入邊界條件和激勵建立對應(yīng)的電磁仿真模型。
8.b.對步驟a所建電磁仿真模型采用四面體網(wǎng)格剖分求解域,獲得四面體網(wǎng)格節(jié)點的坐標(biāo)信息。
9.c.采用矢量基函數(shù),進行標(biāo)準(zhǔn)的有限元電磁仿真分析得到步驟b獲得的四面體網(wǎng)格上的電場。
10.d.基于步驟b獲得的四面體網(wǎng)格節(jié)點坐標(biāo)計算四面體網(wǎng)格四個面的重心坐標(biāo),基于步驟c得到的有限元解插值得到重心位置的電場。
11.e.基于步驟d獲得的四面體網(wǎng)格四個面的重心坐標(biāo)以及重心處的電場,采用最小二乘法獲得四面體網(wǎng)格上的電場重構(gòu)一階線性擬合表達式。
12.f.基于四面體網(wǎng)格節(jié)點坐標(biāo)和步驟e獲得的電場重構(gòu)一階線性擬合表達式,計算得到四面體網(wǎng)格節(jié)點上的電場恢復(fù)解。
13.g.基于步驟f得到的電場恢復(fù)解進行后驗誤差估計,得到四面體網(wǎng)格加密指示,并對四面體網(wǎng)格進行加密,得到加密的四面體網(wǎng)格及其節(jié)點的坐標(biāo)信息。
14.h.重復(fù)步驟c至步驟g,直到有限元電磁仿真分析的計算結(jié)果滿足精度要求。
15.本發(fā)明首先對目標(biāo)微波元器件進行有限元建模,引入邊界條件和激勵建立對應(yīng)的電磁仿真模型;然后,采用四面體網(wǎng)格剖分求解域,對模型進行有限元電磁仿真分析,計算出四面體網(wǎng)格四個面的重心處的電場,利用重心處的電場,采用最小二乘原理重新擬合出四面體網(wǎng)格上的電場重構(gòu)一階線性擬合表達式;接著利用重構(gòu)擬合表達式計算出節(jié)點處的恢復(fù)解,結(jié)合節(jié)點處的電場,進行后驗誤差估計;最后根據(jù)四面體網(wǎng)格上的誤差對網(wǎng)格進行加密,加密后再進行有限元電磁仿真分析,直至有限元解符合精度要求。
16.綜上所述,本發(fā)明中,通過采用最小二乘法,基于單個四面體網(wǎng)格上的有限元解和四面體網(wǎng)格的坐標(biāo)信息即可實現(xiàn)單個四面體網(wǎng)格上恢復(fù)解的構(gòu)造,無需額外的信息;且以單個四面體為最小實施單元,也不需要和其它四面體網(wǎng)格進行數(shù)據(jù)交互,因此信息相對集中,避免了在邊界上需要特殊處理的問題,提高了普適性。本發(fā)明方法工程實現(xiàn)較簡單,計算量小,普適性高。
附圖說明
17.圖1是本發(fā)明的流程圖;
18.圖2是實施例的模型圖;
19.圖3是實施例的四面體網(wǎng)格;
20.圖4是實施例自適應(yīng)前后的網(wǎng)格數(shù)對比圖。
具體實施方式
21.下面結(jié)合附圖和實施例來詳細說明本發(fā)明的技術(shù)方案。
22.參照圖1,一種基于恢復(fù)型后驗誤差估計的網(wǎng)格自適應(yīng)方法,包含以下步驟:
23.a.將目標(biāo)微波元器件進行有限元建模,引入邊界條件和激勵建立對應(yīng)的電磁仿真模型。
24.本發(fā)明實施例以魔t的電磁傳輸分析為例,建立如圖2所示的模型結(jié)構(gòu),引入4個波端口激勵,模型邊界為理想電邊界。
25.b.對步驟a所建電磁仿真模型采用四面體網(wǎng)格剖分求解域,獲得四面體網(wǎng)格節(jié)點的坐標(biāo)信息。
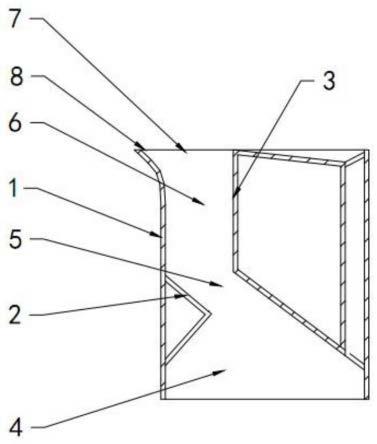
26.采用四面體網(wǎng)格剖分計算域模型是有限元方法中的一種公知過程,因此本步驟不再詳細描述,笛卡爾坐標(biāo)系下,四面體網(wǎng)格節(jié)點如圖3所示表示為1,2,3,4四個節(jié)點。
27.c.采用矢量基函數(shù),進行標(biāo)準(zhǔn)的有限元電磁仿真分析得到步驟b獲得的四面體網(wǎng)格上的電場。
28.本問題的控制方程為矢量波動方程,試探函數(shù)為一階矢量基函數(shù)有限元電磁
仿真分析是一種公知的過程,此處不再詳細闡述。基于棱邊的有限元解和矢量基函數(shù),插值得到四面體網(wǎng)格上任意點的矢量電場為:
[0029][0030]
其中,是第e個四面體網(wǎng)格第j條邊的基函數(shù),是第e個四面體網(wǎng)格第j條邊的解,x,y,z為笛卡爾坐標(biāo)系的三個坐標(biāo)方向分量。
[0031]
d.基于步驟b獲得的四面體網(wǎng)格節(jié)點坐標(biāo)計算四面體網(wǎng)格四個面的重心坐標(biāo),基于步驟c得到的有限元解插值得到重心位置的電場;
[0032]
如圖3所示,四面體四個面分別命名為f1,f2,f3,f4,其中f1為節(jié)點2、3、4連線組成的面,其中f2為節(jié)點1、3、4連線組成的面,其中f3為節(jié)點1、2、4連線組成的面,其中f4為節(jié)點1、2、3連線組成的面。四面體網(wǎng)格四個面的重心表示為5,6,7,8四個點,其中點5為面f1的重心點,點6為面f2的重心點,點7為面f3的重心點,點8為面f4的重心點。
[0033]
四面體網(wǎng)格面f1的重心坐標(biāo)為
[0034]
x5=(x2+x3+x4)/3,y5=(y2+y3+y4)/3,z5=(z2+z3+z4)/3
??
(2)
[0035]
四面體網(wǎng)格面f2的重心坐標(biāo)為
[0036]
x6=(x1+x3+x4)/3,y6=(y1+y3+y4)/3,z6=(z1+z3+z4)/3
??
(3)
[0037]
四面體網(wǎng)格面f3的重心坐標(biāo)為
[0038]
x7=(x1+x2+x4)/3,y7=(y1+y2+y4)/3,z7=(z1+z2+z4)/3
??
(4)
[0039]
四面體網(wǎng)格面f4的重心坐標(biāo)為
[0040]
x8=(x1+x2+x3)/3,y8=(y1+y2+y3)/3,z8=(z1+z2+z3)/3
??
(5)
[0041]
將重心坐標(biāo)代入公式(1),得到四面體四個面f1,f2,f3,f4重心處的電場分別為重心處的電場分別為
[0042]
e.基于步驟d獲得的四面體網(wǎng)格四個面的重心坐標(biāo)以及重心處的電場,采用最小二乘法獲得四面體網(wǎng)格上的電場重構(gòu)一階線性擬合表達式。
[0043]
四面體網(wǎng)格上的電場為矢量,且x,y,z各個方向分量值為復(fù)數(shù),因此需要對x,y,z三個方向的分量及其實部和虛部總計6個分量分別進行一階線性擬合,獲得電場重構(gòu)表達式。這6個分量的重構(gòu)表達式構(gòu)造方法一樣,這里以x方向分量的實部f為例,進行詳細說明。
[0044]
構(gòu)造如下格式的一階線性擬合表達式
[0045]
f=a+bx+cy+dz
???????????????????????????
(6)
[0046]
其中a,b,c,d為待求系數(shù),將四面體網(wǎng)格四個面f1,f2,f3,f4重心處的電場x方向分量的實部值以及重心坐標(biāo)代入(6)式,得到表達式在四面體網(wǎng)格四個面的重心點的殘差平方和為:
[0047][0048]
其中fi表示四面體網(wǎng)格四個面f1,f2,f3,f4重心處的電場x方向分量的實部值,s是擬合數(shù)據(jù)的殘差平方和。
[0049]
令殘差平方和s最小,即:
[0050][0051]
求解方程組(8),即可得到擬合表達式(6)的系數(shù)。
[0052]
f.基于四面體網(wǎng)格節(jié)點坐標(biāo)和步驟e獲得的電場重構(gòu)一階線性擬合表達式,計算得到四面體網(wǎng)格節(jié)點上的電場恢復(fù)解。
[0053]
根據(jù)擬合表達式(6)和四面體網(wǎng)格節(jié)點處的坐標(biāo),計算出節(jié)點1,2,3,4處的擬合電場(即恢復(fù)解)其中上標(biāo)“*”表示電場是重構(gòu)的,一般稱其為恢復(fù)解。
[0054]
g.基于步驟f得到的電場恢復(fù)解進行后驗誤差估計,得到四面體網(wǎng)格加密指示,并對四面體網(wǎng)格進行加密,得到加密的四面體網(wǎng)格及其節(jié)點的坐標(biāo)信息。
[0055]
根據(jù)(1)式計算出節(jié)點1,2,3,4處的電場結(jié)合恢復(fù)解結(jié)合恢復(fù)解得到第e個四面體網(wǎng)格后驗誤差范數(shù)||ξe||為
[0056][0057]
其中||表示取模值,ve為第e個四面體網(wǎng)格的體積,為節(jié)點1,2,3,4處恢復(fù)解在x,y,z三個方向上的分量,為節(jié)點1,2,3,4處電場在x,y,z三個方向上的分量。
[0058]
計算所有四面體網(wǎng)格的后驗誤差,采用網(wǎng)格加密策略進行網(wǎng)格加密判斷,獲得需要加密的四面體網(wǎng)格,并計算對應(yīng)網(wǎng)格的加密指示。根據(jù)加密指示對網(wǎng)格進行加密,獲得加密的四面體網(wǎng)格及其節(jié)點的坐標(biāo)信息,這是一種公知過程,因此本步驟不再詳細描述。
[0059]
h.重復(fù)步驟c至步驟g,直到有限元電磁仿真分析的計算結(jié)果滿足精度要求。
[0060]
圖4展示了本實施例自適應(yīng)前后的網(wǎng)格的對比,結(jié)果表明本發(fā)明能夠?qū)崿F(xiàn)網(wǎng)格自適應(yīng)加密。
[0061]
通過以上實施例可見,本發(fā)明首先獲取單個四面體網(wǎng)格上的有限元解和四面體網(wǎng)格的坐標(biāo)信息,再結(jié)合最小二乘法,即可實現(xiàn)單個四面體網(wǎng)格上恢復(fù)解的構(gòu)造,無需額外的信息;且整個方法中以單個四面體為最小實施單元,因此不需要和其它四面體網(wǎng)格進行數(shù)據(jù)交互,信息相對集中,避免了在邊界上需要特殊處理的問題,提高了普適性。本發(fā)明具有工程實現(xiàn)較簡單,計算量小,以及普適性高的優(yōu)點。